题目内容
5．已知$\sqrt{5}$≈2.236，求5$\sqrt{\frac{1}{5}}$-$\frac{5}{4}$$\sqrt{\frac{4}{5}}$+$\sqrt{45}$的近似值（结果保留小数点后两位）．分析 原式各项化为最简二次根式，合并后取近似值即可．
解答 解：原式=5×$\frac{\sqrt{5}}{5}$-$\frac{1}{2}$$\sqrt{5}$+3$\sqrt{5}$=$\frac{7}{2}$$\sqrt{5}$≈7.83．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点，若CF∥AB，则CD与AF的关系为相等．
16．
假期里，小红和小慧去买菜，三次购买的西红柿价格和数量如下表：
（1）小红和小慧购买西红柿数量的中位数是2，众数是2；
（2）从平均价格看，谁买的西红柿要便宜些．
小亮的说法
小明的说法
思考小亮和小明的说法，你认为谁说得对？为什么？
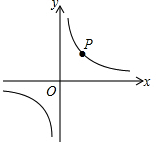
（3）小明在直角坐标系中画出反比例函数的图象，图象经过点P（如图），点P的横、纵坐标分别为小红和小慧购买西红柿价格的平均数．
①求此反比例函数的关系式；
②判断点Q（2，5）是否在此函数图象上．
假期里，小红和小慧去买菜，三次购买的西红柿价格和数量如下表：| 单价/（元/千克） | 4 | 3 | 2 | 合计 |
| 小红购买的数量/千克 | 1 | 2 | 3 | 6 |
| 小慧购买的数量/千克 | 2 | 2 | 2 | 6 |
（2）从平均价格看，谁买的西红柿要便宜些．
小亮的说法
| 每次购买单价相同，购买总量也相同，平均价格应该也一样，都是（4+3+2）÷3=3（元/千克），所以两人购买的西红柿一样便宜． |
| 购买的总量虽然相同，但小红花了16元，小慧花了18元，平均价格不一样，所以购买的西红柿便宜 |
（3）小明在直角坐标系中画出反比例函数的图象，图象经过点P（如图），点P的横、纵坐标分别为小红和小慧购买西红柿价格的平均数．
①求此反比例函数的关系式；
②判断点Q（2，5）是否在此函数图象上．
如图，△ABC中，∠B=2∠C，AD⊥BC于D，M是BC的中点，求证：AB=2DM．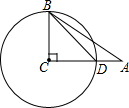
如图，在△ABC中，已知∠C=90°，sinA=$\frac{3}{5}$，以BC为半径的⊙C交AC边上一点D，若AD=4，求半径BC的长．
如图，已知?ABCD中，P是∠B、∠C的平分线上的交点，PM⊥BC于M，若BP=4+$\sqrt{2}$，CP=4-$\sqrt{2}$，求PM的长．
如图2、图3，AB∥EF，∠D与∠B，∠EFD有何数量关系？