题目内容
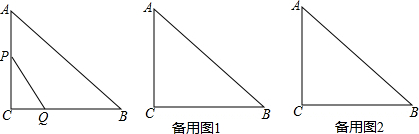
8.如图,在正方形ABCD中,BD为对角线,(1)如图1,E、P为直线BC上两点,连接DP、DE,若点E为BC中点,BC=2,当∠DPC=∠EDC时,求△PED的面积;
(2)如图2,E在BD上,且∠ECD=15°,过C作CP⊥CE交DB延长线于P,在CP上取点F,连接EF,延长EC至点G使CG=CF,在CP上取点H,连接GH使GH=EF.求证:2DE=PH.

分析 (1)如图1中,由△ECD∽△DCP,得$\frac{DC}{CP}$=$\frac{EC}{DC}$,求出PC,再根据S△PDE=$\frac{1}{2}$•PE•DC计算即可.
(2)如图2中,连接BH.由△ECF≌△HCG,推出EC=HC,再证明∠P=30°,由△BCH≌△DCE,推出DE=BH,∠CBH=∠CDE=45°,推出∠DBH=∠DBC+∠CBH=90°,推出∠FBH=90°,推出PH=2BH即可解决问题.
解答 解:(1)如图1中,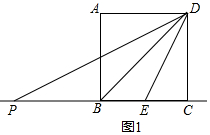
∵四边形ABCD是正方形,
∴CD=BC=2,∠DCB=90°,
∵点E为BC中点,
∴EC=1,
∵∠DPC=∠EDC,∠DCE=∠DCP,
∴△ECD∽△DCP,
∴$\frac{DC}{CP}$=$\frac{EC}{DC}$,
∴$\frac{2}{PC}$=$\frac{1}{2}$,
∴PC=4,PE=3,
∴S△PDE=$\frac{1}{2}$•PE•DC=$\frac{1}{2}$×3×2=3.
(2)如图2中,连接BH.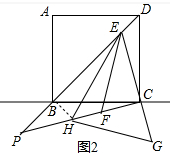
∵CE⊥PC,
∴∠ECF=∠HCG=90°,
在△ECF和△HCG中,
$\left\{\begin{array}{l}{EC=CH}\\{∠ECF=∠HCG}\\{CF=CG}\end{array}\right.$,
∴△ECF≌△HCG,
∴EC=HC,
∵∠DCE=∠BCD=90°,
∴∠ECD=∠BCH=15°,
∵∠DBC=∠BCP+∠P=45°,
∴∠P=30°,
在△BCH和△DCE中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCH=∠ECD}\\{CH=CE}\end{array}\right.$,
∴△BCH≌△DCE,
∴DE=BH,∠CBH=∠CDE=45°,
∴∠DBH=∠DBC+∠CBH=90°,
∴∠FBH=90°,
∴PH=2BH,
∴PH=2DE.
点评 本题考查正方形的性质、全等三角形的判定和性质,直角三角形的30度角性质等知识,解题的关键是正确寻找全等三角形解决问题,证明线段之间的两倍关系要想到直角三角形30度角性质,属于中考常考题型.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
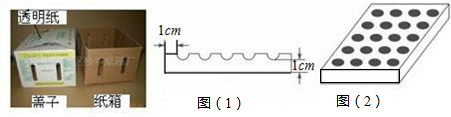
仁爱英语同步练习册系列答案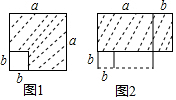 如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a+b)2=a2+2ab 十b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | (a+2b)(a-b)═a2+ab-2b2 |
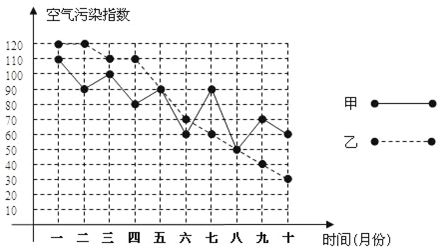
(1)填写下表:
| 平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
| 甲 | 80 | 340 | 1 | |
| 乙 | 1060 | 80 | 3 |
①从平均数和空气质量为优的次数来分析:空气质量为优的次数甲城市比乙城市少;(填“多”或“少),乙城市的空气质量比甲城市的空气质量好些.(填“好些”或“差些”);
②从平均数和中位数来分析:甲的中位数<乙的中位数(填“=”、“>”或“<”),空气质量相对较好的城市是乙(填“甲”或“乙”);
③从平均数和方差来分析:S甲2<S乙2,空气污染指数比较稳定的城市是甲(填“甲”或“乙”);
④根据折线图上两城市的空气污染指数的走势来分析,两城市治理环境污染的效果较好的城市是乙(填“甲”或“乙”).
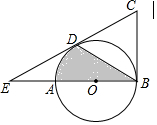 如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.