题目内容
18.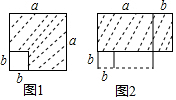 如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a+b)2=a2+2ab 十b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | (a+2b)(a-b)═a2+ab-2b2 |
分析 分别表示出两个图形的阴影部分的面积,即可得出选项.
解答 解:根据图形可知:第一个图形阴影部分的面积为a2-b2,第二个图形阴影部分的面积为(a+b)(a-b),
即a2-b2=(a+b)(a-b),
故选A.
点评 本题考查了平方差公式的应用,能正确表示阴影部分的面积是解此题的关键.

练习册系列答案
相关题目
13.下列各近似数精确到万位的是( )
| A. | 8200 | B. | 8亿5千万 | C. | 4×104 | D. | 12.5×104 |
3.2016年全国两会在北京召开,在开会前,工作人员进行会场布置时在主席台上由两人拉着一条绳子,然后以“准绳”使摆放的茶杯整齐,这样做的理由是( )
| A. | 两点之间线段最短 | B. | 两点确定一条直线 | ||
| C. | 垂线段最短 | D. | 过一点可以作无数条直线 |
7. 如图,在△ABC中,AB=AC,∠A=80°,BD平分∠ABC,则∠BDC的度数为( )
如图,在△ABC中,AB=AC,∠A=80°,BD平分∠ABC,则∠BDC的度数为( )
 如图,在△ABC中,AB=AC,∠A=80°,BD平分∠ABC,则∠BDC的度数为( )
如图,在△ABC中,AB=AC,∠A=80°,BD平分∠ABC,则∠BDC的度数为( )| A. | 100° | B. | 65° | C. | 75° | D. | 105° |
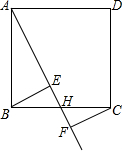 如图,在正方形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
如图,在正方形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.