题目内容
2．
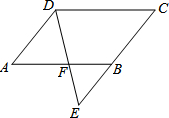已知：如图，?ABCD中，E是CB延长线上一点，DE交AB于F．求证：AD•CD=AF•CE．
分析 根据已知条件就可推出△ECD∽△DAF，根据相似三角形的性质得到对应边的比例式，即可得到结论．
解答 证明：在?ABCD中，
∵AB∥DC，
∴∠CDE=∠AFD，
∵∠A=∠C，
∴△ECD∽△DAF，
∴$\frac{CD}{AF}=\frac{CE}{AD}$，
∴AD•CD=AF•CE．
点评 本题主要考查相似三角形的判定与性质、平行四边形的性质，本题的关键是证明△ECD和△DAF相似．
练习册系列答案
相关题目
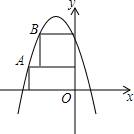如图，在平面直角坐标系中，沿着两条坐标轴摆着两个相同的矩形，其长、宽分别为2，1，抛物线y=-x2+bx+c经过A、B两点，则b=-1，c=3．
如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为12和8时，则阴影部分的面积为（ ）
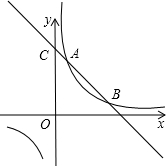如图，一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的交于点A（1，4）和点B，与y轴交于点C（0，5）．求：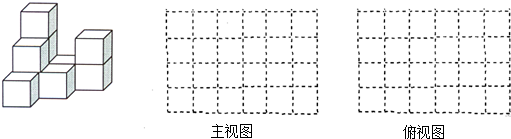
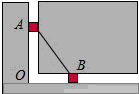图中的两个滑块A，B由一个连杆连接，分别可以在垂直和水平的滑道上滑动．开始时，滑块A距O点20厘米，滑块B距O点15厘米．问：当滑块A向下滑到O点时，滑块B滑动了10厘米．