题目内容
12.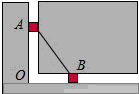 图中的两个滑块A,B由一个连杆连接,分别可以在垂直和水平的滑道上滑动.开始时,滑块A距O点20厘米,滑块B距O点15厘米.问:当滑块A向下滑到O点时,滑块B滑动了10厘米.
图中的两个滑块A,B由一个连杆连接,分别可以在垂直和水平的滑道上滑动.开始时,滑块A距O点20厘米,滑块B距O点15厘米.问:当滑块A向下滑到O点时,滑块B滑动了10厘米.
分析 根据勾股定理求出AB的长,根据题意和图形计算即可.
解答 解:由勾股定理得,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=25厘米,
当滑块A向下滑到O点时,滑块B滑动了25厘米-15厘米=10厘米,
故答案为:10.
点评 本题考查的是勾股定理的应用,善于观察题目的信息,灵活运用勾股定理是解题的关键.

练习册系列答案
相关题目
3.二次函数y=x2+4x-5的图象的对称轴为( )
| A. | 直线x=2 | B. | 直线x=-2 | C. | 直线x=4 | D. | 直线x=-4 |
20.在Rt△ABC中,∠C=90°,BC=1,那么AB的长为( )
| A. | sinA | B. | cosA | C. | $\frac{1}{cosA}$ | D. | $\frac{1}{sinA}$ |
17. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
2.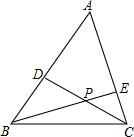 如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=85°,则∠DPE=( )
如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=85°,则∠DPE=( )
 如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=85°,则∠DPE=( )
如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=85°,则∠DPE=( )| A. | 100° | B. | 130° | C. | 120° | D. | 95° |
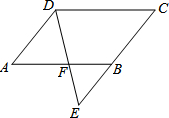 已知:如图,?ABCD中,E是CB延长线上一点,DE交AB于F.求证:AD•CD=AF•CE.
已知:如图,?ABCD中,E是CB延长线上一点,DE交AB于F.求证:AD•CD=AF•CE. 已知:如图,D是BC上一点,△ABC∽△ADE,求证:∠1=∠2=∠3.
已知:如图,D是BC上一点,△ABC∽△ADE,求证:∠1=∠2=∠3.