题目内容
10.如图,在平面直角坐标系xOy中,定义直线x=m与双曲线yn=$\frac{n}{x}$的交点Am,n(m、n为正整数)为“双曲格点”,双曲线yn=$\frac{n}{x}$在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
(1)①“双曲格点”A2,1的坐标为(2,$\frac{1}{2}$);②若线段A4,3A4,n的长为1个单位长度,则n=7;
(2)图中的曲线f是双曲线y1=$\frac{1}{x}$的一条“派生曲线”,且经过点A2,3,则f的解析式为y=$\frac{1}{x}$+1;
(3)画出双曲线y3=$\frac{3}{x}$的“派生曲线”g(g与双曲线y3=$\frac{3}{x}$不重合),使其经过“双曲格点”A2,a、A3,3、A4,b.
分析 (1)①把x=2代入y=$\frac{1}{x}$即可求得点的纵坐标;
②首先求得A4,3A4,n的坐标,然后根据线段A4,3A4,n的长为1个单位长度即可求得n的值;
(2)把x=2代入y=$\frac{3}{x}$求得点A2,3的坐标,然后设f的解析式为y=$\frac{1}{x}$+k,把点A2,3的坐标代入即可求得k的值,进而求得代数式;
(3)首先求得“双曲格点”A2,a、A3,3、A4,b的坐标,把y=$\frac{3}{x}$进行上下平移或把y=$\frac{3}{x}$沿平行与x轴的直线翻折,进行平移即可求得.
解答 解:(1)①把x=2代入y=$\frac{1}{x}$得:y=$\frac{1}{2}$,
则A的坐标是(2,$\frac{1}{2}$);
②把x=4代入y=$\frac{n}{x}$得y=$\frac{n}{4}$.
根据题意得:(4-2)2+($\frac{n}{4}$-$\frac{1}{2}$)2=1,
解得:n=7.
故答案是:(2,$\frac{1}{2}$),7;
(2)把x=2代入y=$\frac{3}{x}$得y=$\frac{3}{2}$,则点A2,3的坐标是(2,$\frac{3}{2}$).
设f的解析式为y=$\frac{1}{x}$+k,
把(2,$\frac{3}{2}$)代入,得$\frac{3}{2}$=$\frac{1}{2}$+k,
解得:k=1.
则f的解析式是:$y=\frac{1}{x}+1$;
(3)把x=2代入y=$\frac{3}{x}$得y=$\frac{3}{2}$,则A2,a的坐标是(2,$\frac{3}{2}$);
把x=3代入y=$\frac{3}{x}$得y=1,则A3,3的坐标是(3,1);
把x=4代入y=$\frac{3}{x}$得y=$\frac{3}{4}$,则A4,b的坐标是(4,$\frac{3}{4}$).
如图.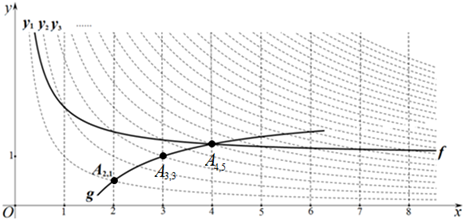
点评 本题考查了反比例函数的图象的平移与翻折以及待定系数法求函数的解析式,理解“派生曲线”和“双曲格点”的定义,理解定义求得“双曲格点”的坐标是关键.

 名校课堂系列答案
名校课堂系列答案| A. | (a3)2÷a5=a10 | B. | (a4)2÷a4=a2 | ||
| C. | (-5a2b3)•(-2a)=10a3b3 | D. | (-a3b)3÷$\frac{1}{2}{a^2}{b^2}=-2{a^4}$b |
| A. | $\frac{1}{2}({b-7})=a+b$ | B. | $\frac{b-7}{2}$=a+b | C. | $\frac{1}{2}$b+7=a+b | D. | $\frac{1}{2}$b-7=a+b |
| A. | 不相交的两条直线叫做平行线 | |
| B. | 相等的角是对顶角 | |
| C. | 过直线外一点有且只有一条直线与已知直线平行 | |
| D. | 过一点有且只有一条直线与已知直线垂直 |
| A. | x1=-2,x2=3 | B. | x1=2,x2=-3 | C. | x1=-1,x2=6 | D. | x1=1,x2=-6 |
| A. | sinA | B. | cosA | C. | $\frac{1}{cosA}$ | D. | $\frac{1}{sinA}$ |
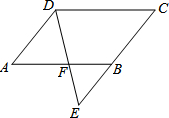 已知:如图,?ABCD中,E是CB延长线上一点,DE交AB于F.求证:AD•CD=AF•CE.
已知:如图,?ABCD中,E是CB延长线上一点,DE交AB于F.求证:AD•CD=AF•CE.