题目内容
1．
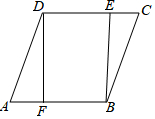如图，已知四边形ABCD是菱形，DF⊥AB于点F，BE⊥CD于点E．（1）求证：AF=CE；
（2）若DE=2，BE=4，求sin∠DAF的值．
分析 （1）根据平行四边形的判定可得四边形BEDF是平行四边形，根据平行四边形的性质可得BF=DE，根据线段的和差关系可得AF=CE；
（2）根据勾股定理可得AF，AD的长，根据三角函数可得sin∠DAF的值．
解答 解：（1）证明：∵四边形ABCD是菱形，
∴AB∥CD，AB=CD，
∵DF⊥AB，BE⊥CD，
∴DF∥BE，
∴四边形BEDF是平行四边形，
∴BF=DE，
∴AF=CE；
（2）∵DE=2，BE=4，
∴设AD=x，则AF=x-2，DF=BE=4，
在Rt△DAF中，x2=42+（x-2）2，
解得x=5，
∴sin∠DAF=$\frac{DF}{AD}$=$\frac{4}{5}$．
点评 考查了菱形的性质，解直角三角形，涉及的知识点有：平行四边形的判定和性质，勾股定理，三角函数，综合性较强，有一定的难度．
练习册系列答案
相关题目
11．为了分析学生数学竞赛成绩，指导老师对全体参赛选手的竞赛成绩进行统计，结果如下（单位；分）；
91 68 73 90 87 71 61 75 82 77 80 82 93 85 76
78 87 74 88 65 72 86 71 69 72 79 81 90 66 70
75 82 77 78 75 85 72 95 80 79 77 78 83 80 83
（1）填写下面的频数分布表．
当分数在60～74时，成绩为及格；当分数在75～84时，成绩为良好；当分数在85～100时，成绩为优秀，请用扇形图表示出及格、良好、优秀所占的百分比．
91 68 73 90 87 71 61 75 82 77 80 82 93 85 76
78 87 74 88 65 72 86 71 69 72 79 81 90 66 70
75 82 77 78 75 85 72 95 80 79 77 78 83 80 83
（1）填写下面的频数分布表．
| 分组 | 划记 | 频数 |
| 60.5～65.5 |  | 2 |
| 65.5～70.5 |  | 4 |
| 70.5～75.5 |   | 10 |
| 75.5～80.5 | 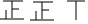 | 12 |
| 80.5～85.5 |  | 8 |
| 85.5～90.5 |  | 6 |
| 90.5～95.5 | 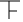 | 3 |
| 合计 |