题目内容
16.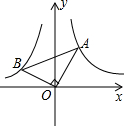 如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.
分析 过A作AN⊥x轴于N,过B作BM⊥x轴于M.设A(x,$\frac{1}{x}$),则ON•AN=1,由tanA=$\frac{\sqrt{3}}{3}$,可得出=$\frac{OB}{OA}$=$\frac{\sqrt{3}}{3}$.通过△MBO∽△NOA的对应边成比例求得k=-OM•BM=-$\frac{1}{3}$.
解答  解:过A作AN⊥x轴于N,过B作BM⊥x轴于M.
解:过A作AN⊥x轴于N,过B作BM⊥x轴于M.
∵第一象限内的点A在反比例函数y的图象上,
∴设A(x,$\frac{1}{x}$)(x>0),ON•AN=1.
∵∠A=30°,
∴tan∠A=$\frac{OB}{OA}$=$\frac{\sqrt{3}}{3}$,
∵OA⊥OB,
∴∠BMO=∠ANO=∠AOB=90°,
∴∠MBO+∠BOM=90°,∠MOB+∠AON=90°,
∴∠MBO=∠AON,
∴△MBO∽△NOA,$\frac{BM}{ON}$=$\frac{OM}{AN}$=$\frac{OB}{OA}$=$\frac{\sqrt{3}}{3}$,
∴BM=$\frac{\sqrt{3}}{3}$ON,OM=$\frac{\sqrt{3}}{3}$AN.
又∵第二象限的点B在反比例函数y=$\frac{k}{x}$上,
∴k=-OM•BM=-$\frac{\sqrt{3}}{3}$ON×$\frac{\sqrt{3}}{3}$AN=-$\frac{1}{3}$.
故答案为-$\frac{1}{3}$.
点评 本题考查了用待定系数法求出反比例函数的解析式,相似三角形的性质和判定的应用,解此题的关键是求出B的坐标.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
7.已知:a=1.8×106,b=1200,计算$\frac{a}{b}$的值等于( )
| A. | 15000 | B. | 1500 | C. | 150 | D. | 15 |
1.已知点(3,-2)在反比例函数y=$\frac{k}{x}$的图象上,则下列点也在该反比例函数y=$\frac{k}{x}$的图象的是( )
| A. | (3,-3) | B. | (-2,3) | C. | (1,6) | D. | (-2,-3) |
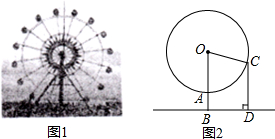 图1是某游乐场的摩天轮,图2是它的正面示意图,已知摩天轮的半径为40米,每分钟绕圆心O匀速旋转15°,其最低点A离地面的距离AB为5米,小明从点A处登上摩天轮,5分钟后旋转到点C,此时小明绕点O旋转了多少度?他离地面的高度CD是多少米?(结果精确到0.1米)
图1是某游乐场的摩天轮,图2是它的正面示意图,已知摩天轮的半径为40米,每分钟绕圆心O匀速旋转15°,其最低点A离地面的距离AB为5米,小明从点A处登上摩天轮,5分钟后旋转到点C,此时小明绕点O旋转了多少度?他离地面的高度CD是多少米?(结果精确到0.1米)