题目内容
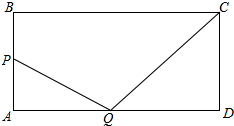 如图,矩形ABCD,AB=6cm,AD=12cm,P是AB上的动点,Q是AD上的动点.P以1cm/s的速度从B到A,Q以2cm/s的速度从A到D,P到A(或Q到D)时停止运动.求PQ+QC最小值.
如图,矩形ABCD,AB=6cm,AD=12cm,P是AB上的动点,Q是AD上的动点.P以1cm/s的速度从B到A,Q以2cm/s的速度从A到D,P到A(或Q到D)时停止运动.求PQ+QC最小值.考点:轴对称-最短路线问题
专题:
分析:设t秒后PQ+QC最小,取点P关于AD的对称点P′,连接CP′与AD相交,根据轴对称确定最短路线问题,交点即为所求的使PQ+QC最小的点Q的位置,表示AP′、AQ、QD,然后根据△AP′Q和△DCQ相似,利用相似三角形对应边成比例列式求出t,再表示出BP′,然后利用勾股定理列式计算即可得解.
解答: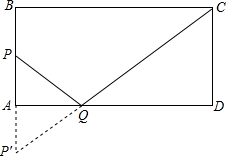 解:设t秒后PQ+QC最小,取点P关于AD的对称点P′,连接CP′与AD相交,
解:设t秒后PQ+QC最小,取点P关于AD的对称点P′,连接CP′与AD相交,
由轴对称确定最短路线问题,交点即为所求的使PQ+QC最小的点Q的位置,
∵AB=6cm,AD=12cm,
∴AP=AP′=6-t,
AQ=2t,QD=12-2t,
∵AB∥CD,
∴△AP′Q∽△DCQ,
∴
=
,
即
=
,
整理得,t2-18t+36=0,
解得t1=9-3
,t2=9+3
(舍去),
所以,BP′=AB+AP′=6+(6-9+3
)=3+3
,
所以,P′C=
=
=3
,
即PQ+QC最小值是3
.
 解:设t秒后PQ+QC最小,取点P关于AD的对称点P′,连接CP′与AD相交,
解:设t秒后PQ+QC最小,取点P关于AD的对称点P′,连接CP′与AD相交,由轴对称确定最短路线问题,交点即为所求的使PQ+QC最小的点Q的位置,
∵AB=6cm,AD=12cm,
∴AP=AP′=6-t,
AQ=2t,QD=12-2t,
∵AB∥CD,
∴△AP′Q∽△DCQ,
∴
| AP′ |
| CD |
| AQ |
| QD |
即
| 6-t |
| 6 |
| 2t |
| 12-2t |
整理得,t2-18t+36=0,
解得t1=9-3
| 5 |
| 5 |
所以,BP′=AB+AP′=6+(6-9+3
| 5 |
| 5 |
所以,P′C=
| BP′2+BC2 |
(3+3
|
22+2
|
即PQ+QC最小值是3
22+2
|
点评:本题考查了轴对称确定最短路线问题,相似三角形的判定与性质,勾股定理的应用,利用轴对称确定出相似三角形并列出比例式是解题的关键.

练习册系列答案
相关题目
某班共有x个学生,其中女生占40%,那么男生人数为( )人.
| A、40%x | ||
| B、(1-40%)x | ||
C、
| ||
D、
|
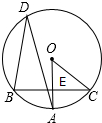 在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧
在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧
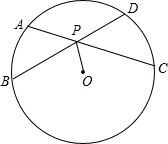 如图,AC、BD为圆O的两条弦,AC、BD相交于点P,连结OP,若OP平分∠BPC,求证:AC=BD.
如图,AC、BD为圆O的两条弦,AC、BD相交于点P,连结OP,若OP平分∠BPC,求证:AC=BD.