题目内容
已知二次函数 的图像如图所示,对称轴是直线x=1,下列结论中:①abc>0 ②2a+b=0 ③b2-4ac<0 ④4a+2b+c>0 ⑤ 3b<2c ,其中正确的是 。
的图像如图所示,对称轴是直线x=1,下列结论中:①abc>0 ②2a+b=0 ③b2-4ac<0 ④4a+2b+c>0 ⑤ 3b<2c ,其中正确的是 。

②④⑤.
【解析】
试题分析:由抛物线开口向上,得到a>0,再由对称轴在y轴右侧,得到a与b异号,可得出b<0,又抛物线与y轴正半轴相交,得到c>0,可得出abc<0,选项①错误;最后由对称轴为直线x=1,利用对称轴公式得到2a+b=0,选项②正确;由抛物线与x轴有2个交点,得到根的判别式b2﹣4ac大于0,故③错误;由x=2时对应的函数值>0,将x=2代入抛物线解析式可得出4a+2b+c大于0,得到选项④正确;最后由对称轴为直线x=1,利用对称轴公式得到a=﹣ b,由x=﹣1时对应的函数值小于0,将x=﹣1代入抛物线解析式可得出y=a﹣b+c<0,即可得出3b<2c,即可得到⑤正确.
b,由x=﹣1时对应的函数值小于0,将x=﹣1代入抛物线解析式可得出y=a﹣b+c<0,即可得出3b<2c,即可得到⑤正确.
试题解析:∵抛物线的开口向上,∴a>0,
∵﹣ >0,∴b<0,
>0,∴b<0,
∵抛物线与y轴交于正半轴,∴c>0,
∴abc<0,①错误;
∵对称轴为直线x=1,∴﹣ =1,即2a+b=0,②正确,
=1,即2a+b=0,②正确,
∵抛物线与x轴有2个交点,∴b2﹣4ac>0,③错误;
∵对称轴为直线x=1,
∴x=2时,y>0,∴4a+2b+c>0,④正确;
∵2a+b=0,∴a=﹣ b,
b,
∵x=﹣1时,y=a﹣b+c>0,
∴﹣ b﹣b+c>0,
b﹣b+c>0,
∴3b<2c,故⑤正确
则其中正确的有②④⑤.
考点:二次函数图象与系数的关系.

练习册系列答案
相关题目
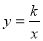 (
(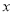 <0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,
<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,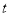 ),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则
),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则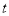 的值是( )
的值是( )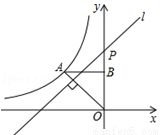
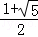 B.
B.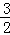 C.
C.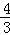 D.
D.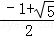
 的一元二次方程x2+4x+2k=0有两个实数根,求
的一元二次方程x2+4x+2k=0有两个实数根,求 的取值范围及
的取值范围及 的非负整数值.
的非负整数值. (k<0)图像的两支分别在( )
(k<0)图像的两支分别在( ) B.
B. ,3 C.6,3 D.
,3 C.6,3 D. ,
, 内有边长分别为a,b,c的三个正方形.则a、b、c满足的关系式是
内有边长分别为a,b,c的三个正方形.则a、b、c满足的关系式是




 ,
, 是一次函数
是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.
 与
与 轴的交点
轴的交点 的坐标及△
的坐标及△ 的面积;
的面积; 的解集(请直接写出答案).
的解集(请直接写出答案).