题目内容
如图,反比例函数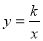 (
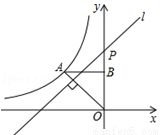
(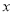 <0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,
<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,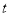 ),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则
),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则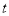 的值是( )
的值是( )
A.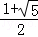 B.
B.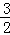 C.
C.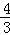 D.
D.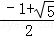
A
【解析】
试题分析:设直线与x轴的交点为点Q,根据题意可得反比例函数的解析式为y=- ,△OAB为等腰直角三角形,则∠AOB=45°,∵PQ⊥OA,∴∠OPQ=45°,点B和点B`关于直线对称,则PB=PB`,BB`⊥PQ,∴∠BPQ=∠B`PQ=45°,即∠B`PQ=90°,∴B`P⊥y轴,∴B`的坐标为(-
,△OAB为等腰直角三角形,则∠AOB=45°,∵PQ⊥OA,∴∠OPQ=45°,点B和点B`关于直线对称,则PB=PB`,BB`⊥PQ,∴∠BPQ=∠B`PQ=45°,即∠B`PQ=90°,∴B`P⊥y轴,∴B`的坐标为(- ,t),∵PB=PB`,∴t-1=
,t),∵PB=PB`,∴t-1= ,整理得:
,整理得: -t-1=0,解得:
-t-1=0,解得: ,
, (舍去).
(舍去).
考点:对称图形的性质、反比例函数的性质、一元二次方程的应用.

练习册系列答案
相关题目


 的长等于( )
的长等于( ) B.
B. C.
C. D.
D.


 的图像如图所示,对称轴是直线x=1,下列结论中:①abc>0 ②2a+b=0 ③b2-4ac<0 ④4a+2b+c>0 ⑤ 3b<2c ,其中正确的是 。
的图像如图所示,对称轴是直线x=1,下列结论中:①abc>0 ②2a+b=0 ③b2-4ac<0 ④4a+2b+c>0 ⑤ 3b<2c ,其中正确的是 。