题目内容
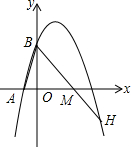 抛物线y=-
抛物线y=-| 5 |
| 6 |
| 7 |
| 6 |
考点:抛物线与x轴的交点,待定系数法求一次函数解析式
专题:
分析:先求出抛物线于x的交点A的坐标和与y轴交点B的坐标,设点M的坐标为(a,0),由MB=MA,列出关于a的方程,求出a的值,即点M的坐标,再由点B的坐标,求出直线BM的解析式.
解答:解:令-
x2+
x+2=0,
解得:x1=-1,x2=
,
∴A(-1,0),B(0,2)
设M(a,0)
∴MA=a+1,MB=
=
∵MA=MB
∴a+1=
解得:a=
∴M(
,0)
设直线BM的解析式为y=kx+b
∴
,解得:
∴直线BM的解析式为y=-
x+2.
| 5 |
| 6 |
| 7 |
| 6 |
解得:x1=-1,x2=
| 12 |
| 5 |
∴A(-1,0),B(0,2)
设M(a,0)
∴MA=a+1,MB=
| OM2+OB2 |
| a2+4 |
∵MA=MB
∴a+1=
| a2+4 |
解得:a=
| 3 |
| 2 |
∴M(
| 3 |
| 2 |
设直线BM的解析式为y=kx+b
∴
|
|
∴直线BM的解析式为y=-
| 4 |
| 3 |
点评:本题考查二次函数与x轴的交点和一次函数解析式的求法,解决问题的关键是根据MA=MB,列出方程求出点M的坐标.

练习册系列答案
相关题目
从车站向东走400m,再向北走500m到小红家;从车站向北走500m,再向西走200m到小强家,若以车站为原点,以正东、正北方向为正方向建立平面直角坐标系,则小红家、小强家的坐标分别为( )
| A、(400,500);(500,200) |
| B、(400,500);(200,500) |
| C、(400,500);(-200,500) |
| D、(500,400);(500,-200) |
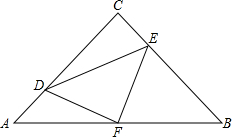 如图,在Rt△ABC中,AC=BC,∠C=90°,AB=8,点F是AB边的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连接DE、DF、EF.在此运动变化的过程中,下列结论中正确的结论是
如图,在Rt△ABC中,AC=BC,∠C=90°,AB=8,点F是AB边的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连接DE、DF、EF.在此运动变化的过程中,下列结论中正确的结论是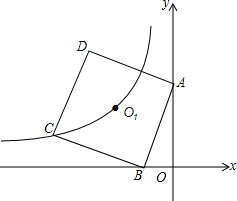 如图,B(-1,0),正方形ABCD中心为O,双曲线y=
如图,B(-1,0),正方形ABCD中心为O,双曲线y= 如图,OA⊥OB,CO⊥DO,
如图,OA⊥OB,CO⊥DO, 如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,AF与BE交于点G,CE和DF交于点H,使得EF与HG互相平分,试说明理由.
如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,AF与BE交于点G,CE和DF交于点H,使得EF与HG互相平分,试说明理由. 如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?
如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?