题目内容
 已知 四边形ABCD中,∠ABD=∠CBD=∠ACD=30°,BE=4,DE=2,则S△ABC=
已知 四边形ABCD中,∠ABD=∠CBD=∠ACD=30°,BE=4,DE=2,则S△ABC=考点:含30度角的直角三角形
专题:
分析:作DF⊥AC.利用相似三角形△DCE∽△BDC的对应边成比例得到DC的长度;然后利用三角函数的定义和勾股定理逆定理推知△ABC为直角三角形.根据三角形的面积公式进行解答即可.
解答: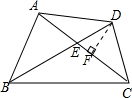 解:作DF⊥AC.
解:作DF⊥AC.
∵∠DCA=∠DBC,∠BDC=∠BDC=30°,
∴△DCE∽△BDC,
∴DC:DE=BD:DC,
∵BE=4,DE=2,
∴DC=2
,
∴DF=
,CF=3
∵sin∠DEF=
=
,
∴∠DEF=60°,
∴∠EDF=30°.
∴EF=
ED=1,∠AEB=60°且∠BAE=30°,
∴∠BAE=90° 且BE=4,
∴AE=2,AB=2
,
∴S△ABC=
AB×AC=6
.
故答案是:6
.
 解:作DF⊥AC.
解:作DF⊥AC.∵∠DCA=∠DBC,∠BDC=∠BDC=30°,
∴△DCE∽△BDC,
∴DC:DE=BD:DC,
∵BE=4,DE=2,
∴DC=2
| 3 |
∴DF=
| 3 |
∵sin∠DEF=
| DF |
| DE |
| ||
| 2 |
∴∠DEF=60°,
∴∠EDF=30°.
∴EF=
| 1 |
| 2 |
∴∠BAE=90° 且BE=4,
∴AE=2,AB=2
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
故答案是:6
| 3 |
点评:本题考查了勾股定理,等腰三角形的性质,含30度角的直角三角形性质的应用,解此题的关键是构造直角三角形,难度适中.

练习册系列答案
相关题目
从车站向东走400m,再向北走500m到小红家;从车站向北走500m,再向西走200m到小强家,若以车站为原点,以正东、正北方向为正方向建立平面直角坐标系,则小红家、小强家的坐标分别为( )
| A、(400,500);(500,200) |
| B、(400,500);(200,500) |
| C、(400,500);(-200,500) |
| D、(500,400);(500,-200) |
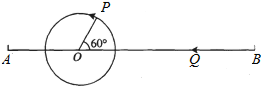 如图,A、B两地相距28个单位长度.AO=8个单位长度,PO=4个单位长度,∠POB=60°,现在点P开始绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q自点B沿BA向点A运动,设点P、Q运动的时间为t(秒).
如图,A、B两地相距28个单位长度.AO=8个单位长度,PO=4个单位长度,∠POB=60°,现在点P开始绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q自点B沿BA向点A运动,设点P、Q运动的时间为t(秒).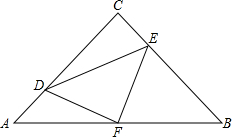 如图,在Rt△ABC中,AC=BC,∠C=90°,AB=8,点F是AB边的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连接DE、DF、EF.在此运动变化的过程中,下列结论中正确的结论是
如图,在Rt△ABC中,AC=BC,∠C=90°,AB=8,点F是AB边的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连接DE、DF、EF.在此运动变化的过程中,下列结论中正确的结论是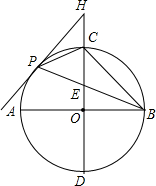 已知,如图,AB,CD是半径为4的⊙O的两条直径,CD⊥AB,点P是
已知,如图,AB,CD是半径为4的⊙O的两条直径,CD⊥AB,点P是
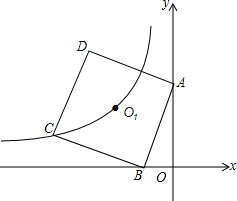 如图,B(-1,0),正方形ABCD中心为O,双曲线y=
如图,B(-1,0),正方形ABCD中心为O,双曲线y= 已知线段a,b,∠α,求作:△ABC,AB=a,AC=b,∠BAC=∠α
已知线段a,b,∠α,求作:△ABC,AB=a,AC=b,∠BAC=∠α