题目内容
 如图,AB为⊙O的直径,C为AE的中点,连结AE交BC于F点.
如图,AB为⊙O的直径,C为AE的中点,连结AE交BC于F点.(1)求证:AC2=CF•CB;
(2)延长AE至D点,若FD=FB=4,CF=2,试判断BD与⊙O的位置关系,并说明理由.
考点:切线的判定,相似三角形的判定与性质
专题:证明题
分析:(1)先利用圆周角定理得到∠ABC=∠CAE,再证明△CAF∽△CBA,利用相似比和比例的性质即可得到AC2=CF•CB;
(2)先利用(1)的结论计算出AC=2
,再根据圆周角定理得∠ACB=90°,利用特殊角的三角函数值可求出∠ABC=30°,则∠CAE=30°,易得∠AFC=∠BFD=60°,接着判定△FBD为等边三角形,得到∠FBD=60°,所以∠ABD=∠ABC+∠FBD=90°,然后根据切线的判定定理可判断BD为⊙O的切线.
(2)先利用(1)的结论计算出AC=2
| 3 |
解答:(1)证明:∵C为AE的中点,
∴
=
,
∴∠ABC=∠CAE,
而∠ACF=∠BCA,
∴△CAF∽△CBA,
∴CA:CB=CF:CA
∴AC2=CF•CB;
(2)解:BD与⊙O相切.理由如下:
∵CB=CF+FB=6,CF=2,
∴AC2=CF•CB=2×6,即AC=2
,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴tan∠ABC=
=
=
,
∴∠ABC=30°,
∴∠CAE=30°,
∴∠AFC=60°,
∴∠BFD=60°,
而FB=FD,
∴△FBD为等边三角形,
∴∠FBD=60°,
∴∠ABD=∠ABC+∠FBD=90°,
∴AB⊥BD,
∴BD为⊙O的切线.
∴
 |
| AC |
 |
| CE |
∴∠ABC=∠CAE,
而∠ACF=∠BCA,
∴△CAF∽△CBA,
∴CA:CB=CF:CA
∴AC2=CF•CB;
(2)解:BD与⊙O相切.理由如下:
∵CB=CF+FB=6,CF=2,
∴AC2=CF•CB=2×6,即AC=2
| 3 |
∵AB为⊙O的直径,
∴∠ACB=90°,
∴tan∠ABC=
| AC |
| BC |
2
| ||
| 6 |
| ||
| 3 |
∴∠ABC=30°,
∴∠CAE=30°,
∴∠AFC=60°,
∴∠BFD=60°,
而FB=FD,
∴△FBD为等边三角形,
∴∠FBD=60°,
∴∠ABD=∠ABC+∠FBD=90°,
∴AB⊥BD,
∴BD为⊙O的切线.
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了圆周角定理、相似三角形的判定与性质.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
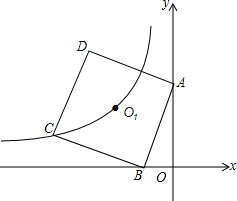 如图,B(-1,0),正方形ABCD中心为O,双曲线y=
如图,B(-1,0),正方形ABCD中心为O,双曲线y= 如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,AF与BE交于点G,CE和DF交于点H,使得EF与HG互相平分,试说明理由.
如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,AF与BE交于点G,CE和DF交于点H,使得EF与HG互相平分,试说明理由.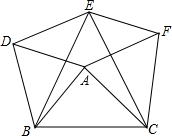 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF,
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF, 已知线段a,b,∠α,求作:△ABC,AB=a,AC=b,∠BAC=∠α
已知线段a,b,∠α,求作:△ABC,AB=a,AC=b,∠BAC=∠α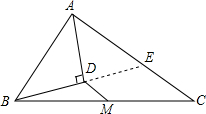 △ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D. 如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?
如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?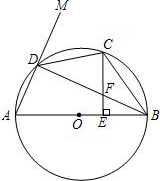 如图,AB是⊙O的直径,C是
如图,AB是⊙O的直径,C是
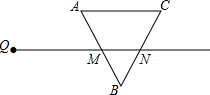 射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,
射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,