题目内容
5．
如图，已知直线a∥b，∠1=55°，则∠2的度数是（ ）| A． | 35° | B． | 55° | C． | 125° | D． | 145° |
分析 根据平行线的性质可得∠1=∠3=55°，再根据邻补角互补可得答案．
解答 
解：∵a∥b，
∴∠1=∠3=55°，
∵∠2+∠3=180°，
∴∠3=180°-∠2=180°-55°=125°，
故选：C．
点评 此题主要考查了平行线的性质，关键是掌握两直线平行，同位角相等．
练习册系列答案
相关题目
16．用反证法证明“同一平面内，若a⊥c，b⊥c，则a∥b”时应假设（ ）
| A． | a不垂直与c | B． | a，b都不垂直与c | C． | a⊥b | D． | a与b相交 |
13．
如图，△ABD≌△CDB，下面四个结论中不正确的是（ ）
如图，△ABD≌△CDB，下面四个结论中不正确的是（ ）| A． | △ABD和△CDB的面积相等 | B． | △ABD和△CDB的周长相等 | ||
| C． | ∠A+∠ABD=∠C+∠CBD | D． | AD∥BC，且AD=BC |
10．
如图，已知在正方形网格中的两个格点三角形是位似形，它们的位似中心是（ ）
如图，已知在正方形网格中的两个格点三角形是位似形，它们的位似中心是（ ）| A． | 点A | B． | 点B | C． | 点C | D． | 点D |
17．
如图，已知a∥b，三角形的直角顶点在直线a上，已知∠1=25°18'27''，则∠2的度数是（ ）
如图，已知a∥b，三角形的直角顶点在直线a上，已知∠1=25°18'27''，则∠2的度数是（ ）| A． | 25°18'27'' | B． | 64° 41'33'' | C． | 74°41'33'' | D． | 64° 41'43'' |
14．
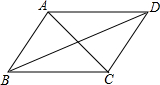如图，下列条件不能够判定AB∥DC的是（ ）
如图，下列条件不能够判定AB∥DC的是（ ）| A． | ∠BAC=∠ACD | B． | ∠DCB+∠ABC=180° | C． | ∠ABD=∠BDC | D． | ∠DAC=∠BCA |
