题目内容
5. 如图,点D在△ABC的一边AC上,且∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有3个.
如图,点D在△ABC的一边AC上,且∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有3个.
分析 由∠C=72゜,∠A=∠DBC=36゜,根据三角形内角和定理与三角形外角的性质,可求得∠ABD=∠A=36°,∠ABC=∠BCD=∠BDC=72°,继而求得答案.
解答 解:∵∠C=72゜,∠A=∠DBC=36゜,
∴∠BDC=180°-∠DBC-∠C=72°=∠C,
∴BC=BD,即△BCD是等腰三角形;
∴∠ABD=∠BDC-∠A=36°=∠A,
∴AD=BD,即△ABD是等腰三角形;
∴∠ABC=∠ABD+∠DBC=72°=∠C,
∴AB=AC,即△ABC是等腰三角形.
故答案为:3.
点评 此题考查了等腰三角形的判定、三角形的外角的性质以及三角形内角和定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
15.若直线y=x-1与抛物线y=x2+5x+a2相交,则它们的交点一定在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
13.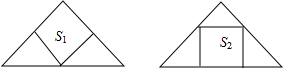 如图,将两张全等的等腰直角三角形纸片按如下两种方法剪成正方形,其面积分别为是S1、S2,则( )
如图,将两张全等的等腰直角三角形纸片按如下两种方法剪成正方形,其面积分别为是S1、S2,则( )
 如图,将两张全等的等腰直角三角形纸片按如下两种方法剪成正方形,其面积分别为是S1、S2,则( )
如图,将两张全等的等腰直角三角形纸片按如下两种方法剪成正方形,其面积分别为是S1、S2,则( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 不能确定 |
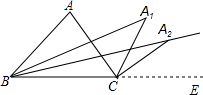 如图所示,△ABC内角∠ABC的平分线与外角∠ACE的角平分线交于点A1.
如图所示,△ABC内角∠ABC的平分线与外角∠ACE的角平分线交于点A1.