题目内容
16．
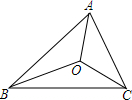如图，△ABC的三边AB、BC、CA长分别是7、8、6，其中三条角平分线相交于点O，将△ABC分为三个小三角形，则S△ABO、S△BCO、S△CAO之间的大小关系是（ ）| A． | S△ABO=S△BCO=S△CAO | B． | S△ABO＞S△BCO＞S△CAO | ||
| C． | S△BCO＞S△ABO＞S△CAO | D． | 不等确定 |
分析 利用角平分线上的一点到角两边的距离相等的性质，可知三个三角形高相等，底分别是7、8、6，所以面积之比就是7：8：6．
解答 解：利用同高不同底的三角形的面积之比就是底之比可知：S△ABO：S△BCO：S△CAO=7：8：6．则S△BCO＞S△ABO＞S△CAO，
故选C．
点评 本题主要考查了角平分线上的一点到两边的距离相等的性质及三角形的面积公式．做题时应用了三个三角形的高时相等的，这点式非常重要的．
练习册系列答案
全优点练单元计划系列答案
相关题目
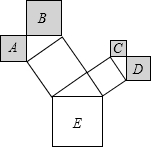如图所示，是一株美丽的勾股树，其中所有三角形都是直角三角形，所有四边形都是正方形．若正方形A、B、C、D的边长为2、4、1、2，则正方形E的面积是（ ）
如图，AB∥A′B′，BC∥B′C′，△AOC与△A′OC′相似吗？为什么？