题目内容
1．计算：（1-$\frac{1}{{5}^{2}}$）（1-$\frac{1}{{6}^{2}}$）（1-$\frac{1}{{7}^{2}}$）…（1-$\frac{1}{200{7}^{2}}$）分析 利用平方差公式展开后计算即可．
解答 解：原式=（1-$\frac{1}{5}$）（1+$\frac{1}{5}$）（1-$\frac{1}{6}$）（1+$\frac{1}{6}$）（1-$\frac{1}{7}$）（1+$\frac{1}{7}$）…（1-$\frac{1}{2007}$）（1+$\frac{1}{2007}$）
=$\frac{4}{5}$×$\frac{6}{5}$×$\frac{5}{6}$×$\frac{7}{6}$×$\frac{6}{7}$×$\frac{8}{7}$×…×$\frac{2006}{2007}$×$\frac{2008}{2007}$
=$\frac{4}{5}$×$\frac{2008}{2007}$
=$\frac{8032}{10035}$．
点评 本题考查了因式分解的应用，解题的关键是能够熟练的掌握平方差公式，难道不大．
练习册系列答案
小题狂做系列答案
相关题目
11．下列等式变形错误的是（ ）
| A． | 由m=n，得m+5=n+5 | B． | 由m=n，得$\frac{m}{-7}$=$\frac{n}{-7}$ | ||
| C． | 由x+2=y+2，得x=y | D． | 由-2x=-2y，得x=-y |
一次函数y=ax+b的图象如图所示，化简|a|+|b|-|a-b|的结果是0．
16．
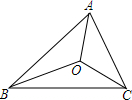如图，△ABC的三边AB、BC、CA长分别是7、8、6，其中三条角平分线相交于点O，将△ABC分为三个小三角形，则S△ABO、S△BCO、S△CAO之间的大小关系是（ ）
如图，△ABC的三边AB、BC、CA长分别是7、8、6，其中三条角平分线相交于点O，将△ABC分为三个小三角形，则S△ABO、S△BCO、S△CAO之间的大小关系是（ ）| A． | S△ABO=S△BCO=S△CAO | B． | S△ABO＞S△BCO＞S△CAO | ||
| C． | S△BCO＞S△ABO＞S△CAO | D． | 不等确定 |
10．
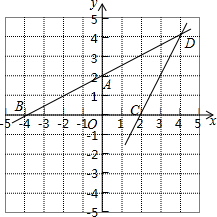如图，直线AB的关系式为0.5x-y=-2，直线CD的关系式为2x-y=4，点D为两条直线的交点，则方程$\left\{\begin{array}{l}{0.5x-y=-2}\\{2x-y=4}\end{array}\right.$的解为（ ）
如图，直线AB的关系式为0.5x-y=-2，直线CD的关系式为2x-y=4，点D为两条直线的交点，则方程$\left\{\begin{array}{l}{0.5x-y=-2}\\{2x-y=4}\end{array}\right.$的解为（ ）| A． | $\left\{\begin{array}{l}{x=0}\\{y=-4}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$ |