题目内容
5. 如图,AB∥A′B′,BC∥B′C′,△AOC与△A′OC′相似吗?为什么?
如图,AB∥A′B′,BC∥B′C′,△AOC与△A′OC′相似吗?为什么?
分析 由平行线分线段成比例定理得出比例式,得出$\frac{OA}{OA′}=\frac{OC}{OC′}$,再由公共角相等,即可得出结论.
解答 解:△AOC与△A′OC′相似;理由如下:
∵AB∥A′B′,BC∥B′C′,
∴$\frac{OA}{OA′}=\frac{OB}{OB′}$,$\frac{OC}{OC′}=\frac{OB}{OB′}$,
∴$\frac{OA}{OA′}=\frac{OC}{OC′}$,
又∵∠AOC=∠A′OC′,
∴△AOC∽△A′OC′.
点评 本题考查了相似三角形的判定、平行线分线段成比例定理;熟练掌握相似三角形的判定方法,由平行线分线段成比例定理得出比例式是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
15.甲以5km/h的速度先走16分钟,乙以13km/h的速度追上甲,则乙追上甲需要的时间为( )
| A. | 1h | B. | 6h | C. | $\frac{1}{6}$h | D. | $\frac{80}{13}$h |
16.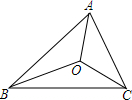 如图,△ABC的三边AB、BC、CA长分别是7、8、6,其中三条角平分线相交于点O,将△ABC分为三个小三角形,则S△ABO、S△BCO、S△CAO之间的大小关系是( )
如图,△ABC的三边AB、BC、CA长分别是7、8、6,其中三条角平分线相交于点O,将△ABC分为三个小三角形,则S△ABO、S△BCO、S△CAO之间的大小关系是( )
 如图,△ABC的三边AB、BC、CA长分别是7、8、6,其中三条角平分线相交于点O,将△ABC分为三个小三角形,则S△ABO、S△BCO、S△CAO之间的大小关系是( )
如图,△ABC的三边AB、BC、CA长分别是7、8、6,其中三条角平分线相交于点O,将△ABC分为三个小三角形,则S△ABO、S△BCO、S△CAO之间的大小关系是( )| A. | S△ABO=S△BCO=S△CAO | B. | S△ABO>S△BCO>S△CAO | ||
| C. | S△BCO>S△ABO>S△CAO | D. | 不等确定 |
10.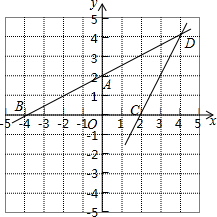 如图,直线AB的关系式为0.5x-y=-2,直线CD的关系式为2x-y=4,点D为两条直线的交点,则方程$\left\{\begin{array}{l}{0.5x-y=-2}\\{2x-y=4}\end{array}\right.$的解为( )
如图,直线AB的关系式为0.5x-y=-2,直线CD的关系式为2x-y=4,点D为两条直线的交点,则方程$\left\{\begin{array}{l}{0.5x-y=-2}\\{2x-y=4}\end{array}\right.$的解为( )
 如图,直线AB的关系式为0.5x-y=-2,直线CD的关系式为2x-y=4,点D为两条直线的交点,则方程$\left\{\begin{array}{l}{0.5x-y=-2}\\{2x-y=4}\end{array}\right.$的解为( )
如图,直线AB的关系式为0.5x-y=-2,直线CD的关系式为2x-y=4,点D为两条直线的交点,则方程$\left\{\begin{array}{l}{0.5x-y=-2}\\{2x-y=4}\end{array}\right.$的解为( )| A. | $\left\{\begin{array}{l}{x=0}\\{y=-4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$ |
15.计算(am+bn)(a2m-b2n)(am-bn)正确的是( )
| A. | a4m-2a2mb2n+b4m | B. | a4m-b4 | C. | a4m+b4n | D. | a2m+b2n+2ambn |