题目内容
14.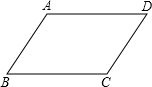 如图,在?ABCD中,AB=8,AD=10,过点A的直线交边BC所在的直线为点E,交DC所在的直线为点F,若CE=2,则DF的长为10或$\frac{20}{3}$.
如图,在?ABCD中,AB=8,AD=10,过点A的直线交边BC所在的直线为点E,交DC所在的直线为点F,若CE=2,则DF的长为10或$\frac{20}{3}$.
分析 此题分两种情况:如图1在?ABCD中,因为AB∥CD,AB=CD,得到△ABE∽△FDE,列比例式解出CF 的长度,即可求出DF,如图2,BE=10+2=12,还是通过△ABE∽△FDE,
得到比例式求出CF的长度,即可求出DF.
解答  解:如图1在?ABCD中,
解:如图1在?ABCD中,
∵AB∥CD,AB=CD,
∴△ABE∽△FDE,
∴$\frac{AB}{CF}$=$\frac{BE}{CE}$,
∵BC=10,CE=2,
∴BE=8,
∴$\frac{8}{CF}$=$\frac{8}{2}$,
∴CF=2,
∴DF=DC+CF=10;
如图2 ,BE=10+2=12,
,BE=10+2=12,
∵△ABE∽△FDE,
∴$\frac{AB}{CF}$=$\frac{BE}{CE}$,
∴$\frac{8}{CF}$=$\frac{12}{2}$,
∴CF=$\frac{4}{3}$,
∴DF=CD-CF=$\frac{20}{3}$.
故答案为:10或$\frac{20}{3}$.
点评 本题考查了平行四边形的性质,相似三角形的判定和性质,正确的作出图形是解题的关键.

练习册系列答案
相关题目
4.已知坐标原点为O,点A(2,1),将OA绕原点O顺时针旋转90°后,A的对应点A1的坐标是( )
| A. | (2,-1) | B. | (-2,1) | C. | (1,-2) | D. | (-1,2) |
2.在下列运算中,正确的是( )
| A. | 4x+2y=6xy | B. | 2x3•x2=2x5 | C. | (x2)3=x5 | D. | (3xy)2÷(xy)=3xy |
19.使$\sqrt{x+1}$有意义的x的取值范围是( )
| A. | x≥-1 | B. | x<1 | C. | x>-1 | D. | x≤1 |
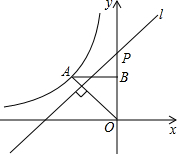 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是$\frac{1+\sqrt{5}}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是$\frac{1+\sqrt{5}}{2}$.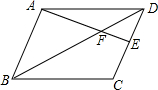 在?ABCD中,点E为CD的中点,连接BD交AE于点F,则AF:FE=2:1.
在?ABCD中,点E为CD的中点,连接BD交AE于点F,则AF:FE=2:1. 已知实数a、b在数轴上的位置如图所示,则化简$\sqrt{(a-b)^{2}}$的结果是-a+b.
已知实数a、b在数轴上的位置如图所示,则化简$\sqrt{(a-b)^{2}}$的结果是-a+b.