题目内容
2. 已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.
已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.(1)求这个函数的解析式及函数图象顶点P的坐标;
(2)画出二次函数的图象(要列表画图)并求四边形OBPA的面积.
分析 (1)设出二次函数的一般式方程,将A、B及C的坐标代入即可确定出解析式,然后化成顶点式即可求得顶点坐标.
(2)通过列表、描点、连线画出函数的图象,在坐标系标出A、B、P点,然后根据梯形的面积和三角形的面积求得即可.
解答 解:(1)设二次函数解析式为y=ax2+bx+c,
将A、B及C坐标代入得:$\left\{\begin{array}{l}{9a+3b+c=0}\\{c=-3}\\{4a-2b+c=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$.
则函数解析式为y=x2-2x-3.
∵y=x2-2x-3=(x-1)2-4,
∴顶点P的坐标(1,-4);
(2)列表:
| x | -1 | 0 | 1 | 2 | 3 |
| y | 0 | -3 | -4 | -3 | 0 |
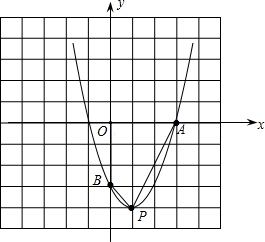
四边形OBPA的面积=$\frac{1}{2}$(3+4)×1+$\frac{1}{2}$×2×4=$\frac{15}{2}$.
点评 此题考查了待定系数法求二次函数的解析式,利用描点法作二次函数图象以及四边形的面积,待定系数法求解析式是解题的关键.

练习册系列答案
相关题目
14.为了从甲乙两名选手中选拔一名参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下两个统计图表:
(1)请补全上述图表;
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?请说明你的理由.

| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 7 | 2.8 | 0 |
| 乙 | 7 | 7.5 | 5.4 | 1 |
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?请说明你的理由.

 如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM.
如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM. 学生会举办摄影展览,在每张长和宽分别为18厘米和12厘米的长方形相片周围镶上一圈等宽的彩纸(如图).经试验彩纸面积为相片面积的$\frac{17}{27}$时较美观,则镶在彩纸条的宽为2.
学生会举办摄影展览,在每张长和宽分别为18厘米和12厘米的长方形相片周围镶上一圈等宽的彩纸(如图).经试验彩纸面积为相片面积的$\frac{17}{27}$时较美观,则镶在彩纸条的宽为2.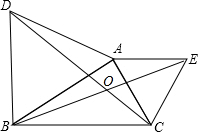 如图,△ABD和△AEC都是等边三角形;
如图,△ABD和△AEC都是等边三角形;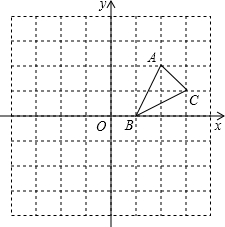 如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立如图所示的平面直角坐标系,△ABC的顶点均在格点上,点B的坐标为(1,0),
如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立如图所示的平面直角坐标系,△ABC的顶点均在格点上,点B的坐标为(1,0), 如图,点N是线段AB上的一个点,AN=6cm,BN=2cm,点M是AB的中点.
如图,点N是线段AB上的一个点,AN=6cm,BN=2cm,点M是AB的中点.