题目内容
7.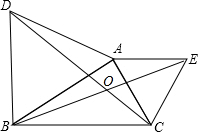 如图,△ABD和△AEC都是等边三角形;
如图,△ABD和△AEC都是等边三角形;(1)求证:BE=CD;
(2)请你用旋转性质证明BE=CD.
分析 (1)利用△ABD、△AEC都是等边三角形,求证△DAC≌△BAE,然后即可得出BE=DC;
(2)利用旋转的性质得出△DAC≌△BAE,然后即可得出BE=DC.
解答 证明:(1)∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°.
∴∠DAC=∠BAC+60°,∠BAE=∠BAC+60°.
∴∠DAC=∠BAE.
在△DAC和△BAE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AE=AC}\end{array}\right.$,
∴△DAC≌△BAE(SAS),
∴BE=DC;
(2)△ABE可以看成是△ADC绕点A逆时针方向旋转60°而得到,
∵CD的对应线段是BE,
∴BE=CD.
点评 此题考查学生对全等三角形的判定与性质和等边三角形的性质的理解与掌握,掌握△DAC≌△BAE的条件是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
19.下列图形中可以作为一个三棱柱的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
16.某通信公司的手机话费标准按原标准每分钟降低a元后,又下调了20%,现在的收费标准是每分钟b元,则原收费标准是每分钟( )
| A. | (a+1.25b)元 | B. | (a-1.25b)元 | C. | (a+5b)元 | D. | (a-5b)元 |

 已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.
已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.