题目内容
20.已知点A,B在数轴上对应的数分别为-4,1.(1)求线段AB的长;
(2)设点P在数轴上对应的数为x,当PA-PB=2时,求x的值;
(3)若点P在A的左侧,M、N分别是PA、PB的中点,当P在A的左侧移动时,求PN-PM的值是否发生改变?若不变,请求其值;若发生变化,请说明理由.
分析 (1)利用距离公示可得结论;
(2)应考虑到A、B、P三点之间的位置关系的多种可能解题;
(3)利用中点性质转化线段之间的倍分关系得出.
解答 解:(1)|AB|=|a-b|=|-4-1|=5;
(2)当P在点A左侧时,
|PA|-|PB|=-(|PB|-|PA|)=-|AB|=-5≠2.
当P在点B右侧时,
|PA|-|PB|=|AB|=5≠2.
∴上述两种情况的点P不存在.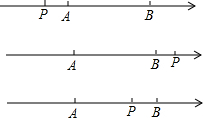
当P在A、B之间时,|PA|=|x-(-4)|=x+4,|PB|=|x-1|=1-x,
∵|PA|-|PB|=2,∴x+4-(1-x)=2.
∴x=-$\frac{1}{2}$,即x的值为-$\frac{1}{2}$;
(3)PN-PM的值不变,值为$\frac{5}{2}$.
∵PN-PM=$\frac{1}{2}$PB-$\frac{1}{2}$PA=$\frac{1}{2}$(PB-PA)=$\frac{1}{2}$AB=$\frac{5}{2}$,
∴PN-PM=$\frac{5}{2}$.
点评 本题主要考查了数轴的相关知识,渗透了分类讨论的思想,利用中点性质转化线段之间的倍分关系是解题的关键.

练习册系列答案
相关题目
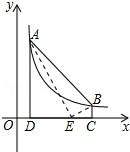 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.



 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.