题目内容
20.问题背景:已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,记△ADM的面积为S1,△BND的面积为S2.(1)初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1•S2=12;
(2)类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1•S2的值;
(3)延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.
(Ⅰ)如图③,当点D在线段AB上运动时,设AD=a,BD=b,求S1•S2的表达式(结果用a,b和α的三角函数表示).
(Ⅱ)如图④,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1•S2的表达式,不必写出解答过程.
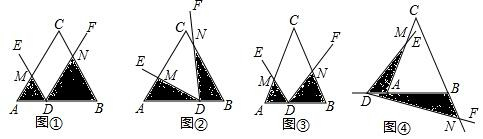
分析 (1)首先证明△ADM,△BDN都是等边三角形,可得S1=$\frac{\sqrt{3}}{4}$•22=$\sqrt{3}$,S2=$\frac{\sqrt{3}}{4}$•(4)2=4$\sqrt{3}$,由此即可解决问题;
(2)如图2中,设AM=x,BN=y.首先证明△AMD∽△BDN,可得$\frac{AM}{BD}$=$\frac{AD}{BN}$,推出$\frac{x}{2}$=$\frac{4}{y}$,推出xy=8,由S1=$\frac{1}{2}$•AD•AM•sin60°=$\sqrt{3}$x,S2=$\frac{1}{2}$DB•sin60°=$\frac{\sqrt{3}}{2}$y,可得S1•S2=$\sqrt{3}$x•$\frac{\sqrt{3}}{2}$y=$\frac{3}{2}$xy=12;
(3)Ⅰ如图3中,设AM=x,BN=y,同法可证△AMD∽△BDN,可得xy=ab,由S1=$\frac{1}{2}$•AD•AM•sinα=$\frac{1}{2}$axsinα,S2=$\frac{1}{2}$DB•BN•sinα=$\frac{1}{2}$bysinα,可得S1•S2=$\frac{1}{4}$(ab)2sin2α.
(Ⅱ)结论不变,证明方法类似;
解答 解:(1)如图1中,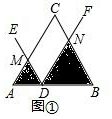
∵△ABC是等边三角形,
∴AB=CB=AC=6,∠A=∠B=60°,
∵DE∥BC,∠EDF=60°,
∴∠BND=∠EDF=60°,
∴∠BDN=∠ADM=60°,
∴△ADM,△BDN都是等边三角形,
∴S1=$\frac{\sqrt{3}}{4}$•22=$\sqrt{3}$,S2=$\frac{\sqrt{3}}{4}$•(4)2=4$\sqrt{3}$,
∴S1•S2=12,
故答案为12.
(2)如图2中,设AM=x,BN=y.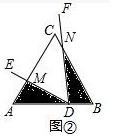
∵∠MDB=∠MDN+∠NDB=∠A+∠AMD,∠MDN=∠A,
∴∠AMD=∠NDB,∵∠A=∠B,
∴△AMD∽△BDN,
∴$\frac{AM}{BD}$=$\frac{AD}{BN}$,
∴$\frac{x}{2}$=$\frac{4}{y}$,
∴xy=8,
∵S1=$\frac{1}{2}$•AD•AM•sin60°=$\sqrt{3}$x,S2=$\frac{1}{2}$DB•sin60°=$\frac{\sqrt{3}}{2}$y,
∴S1•S2=$\sqrt{3}$x•$\frac{\sqrt{3}}{2}$y=$\frac{3}{2}$xy=12.
(3)Ⅰ如图3中,设AM=x,BN=y,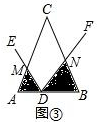
同法可证△AMD∽△BDN,可得xy=ab,
∵S1=$\frac{1}{2}$•AD•AM•sinα=$\frac{1}{2}$axsinα,S2=$\frac{1}{2}$DB•BN•sinα=$\frac{1}{2}$bysinα,
∴S1•S2=$\frac{1}{4}$(ab)2sin2α.
Ⅱ如图4中,设AM=x,BN=y,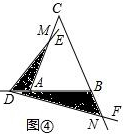
同法可证△AMD∽△BDN,可得xy=ab,
∵S1=$\frac{1}{2}$•AD•AM•sinα=$\frac{1}{2}$axsinα,S2=$\frac{1}{2}$DB•BN•sinα=$\frac{1}{2}$bysinα,
∴S1•S2=$\frac{1}{4}$(ab)2sin2α.
点评 本题考查几何变换综合题、等边三角形的性质、等腰三角形的性质、相似三角形的判定和性质、三角形的面积公式.锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.

| A. | 0.5a>0.5b | B. | -0.5a>-0.5b | C. | a+c<b+c | D. | a-c<b-c |
| A. | x2+2 | B. | x2+3x+2 | C. | x2+3x+3 | D. | x2+2x+2 |
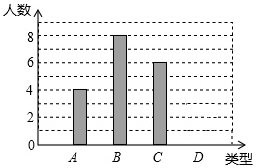 某校300名学生参加植树活动,要求每人植树2-5棵,活动结束后随机抽查了20名学生每人的植树量,并分为四类:A类2棵、B类3棵、C类4棵、D类5棵,将各类的人数绘制成不完整的条形统计图(如图所示),回答下列问题:
某校300名学生参加植树活动,要求每人植树2-5棵,活动结束后随机抽查了20名学生每人的植树量,并分为四类:A类2棵、B类3棵、C类4棵、D类5棵,将各类的人数绘制成不完整的条形统计图(如图所示),回答下列问题: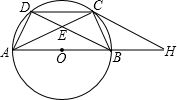 如图,点A,B,C,D是直径为AB的⊙O上的四个点,C是劣弧$\widehat{BD}$的中点,AC与BD交于点E.
如图,点A,B,C,D是直径为AB的⊙O上的四个点,C是劣弧$\widehat{BD}$的中点,AC与BD交于点E.