题目内容
9.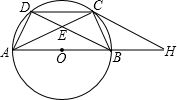 如图,点A,B,C,D是直径为AB的⊙O上的四个点,C是劣弧$\widehat{BD}$的中点,AC与BD交于点E.
如图,点A,B,C,D是直径为AB的⊙O上的四个点,C是劣弧$\widehat{BD}$的中点,AC与BD交于点E.(1)求证:DC2=CE•AC;
(2)若AE=2,EC=1,求证:△AOD是正三角形;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,求△ACH的面积.
分析 (1)由圆周角定理得出∠DAC=∠CDB,证明△ACD∽△DCE,得出对应边成比例,即可得出结论;
(2)求出DC=$\sqrt{3}$,连接OC、OD,如图所示:证出BC=DC=$\sqrt{3}$,由圆周角定理得出∠ACB=90°,由勾股定理得出AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2$\sqrt{3}$,得出OB=OC=OD=DC=BC=$\sqrt{3}$,证出△OCD、△OBC是正三角形,得出∠COD=∠BOC=∠OBC=60°,求出∠AOD=60°,即可得出结论;
(3)由切线的性质得出OC⊥CH,求出∠H=30°,证出∠H=∠BAC,得出AC=CH=3,求出AH和高,由三角形面积公式即可得出答案.
解答 (1)证明:∵C是劣弧$\widehat{BD}$的中点,
∴∠DAC=∠CDB,
∵∠ACD=∠DCE,
∴△ACD∽△DCE,
∴$\frac{AC}{DC}$=$\frac{CD}{CE}$,
∴DC2=CE•AC;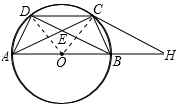
(2)证明:∵AE=2,EC=1,
∴AC=3,
∴DC2=CE•AC=1×3=3,
∴DC=$\sqrt{3}$,
连接OC、OD,如图所示:
∵C是劣弧$\widehat{BD}$的中点,
∴OC平分∠DOB,BC=DC=$\sqrt{3}$,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2$\sqrt{3}$,
∴OB=OC=OD=DC=BC=$\sqrt{3}$,
∴△OCD、△OBC是正三角形,
∴∠COD=∠BOC=∠OBC=60°,
∴∠AOD=180°-2×60°=60°,
∵OA=OD,
∴△AOD是正三角形;
(3)解:∵CH是⊙O的切线,∴OC⊥CH,
∵∠COH=60°,
∴∠H=30°,
∵∠BAC=90°-60°=30°,
∴∠H=∠BAC,
∴AC=CH=3,
∵AH=3$\sqrt{3}$,AH上的高为BC•sin60°=$\frac{3}{2}$,
∴△ACH的面积=$\frac{1}{2}$×3$\sqrt{3}$×$\frac{3}{2}$=$\frac{9\sqrt{3}}{4}$.
点评 本题是圆的综合题目,考查了圆的性质、圆周角定理、相似三角形的判定与性质、正三角形的判定与性质、切线的性质、勾股定理、三角函数、等腰三角形的判定等知识;本题综合性强,有一定难度.

 阅读快车系列答案
阅读快车系列答案| A. | 4和3.5 | B. | 4和3.6 | C. | 5和3.5 | D. | 5和3.6 |
| A. | 此不等式组的正整数解为1,2,3 | B. | 此不等式组的解集为-1<x≤$\frac{7}{6}$ | ||
| C. | 此不等式组有5个整数解 | D. | 此不等式组无解 |
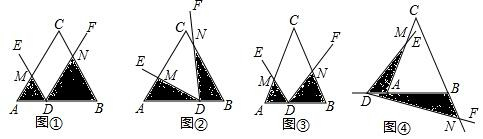
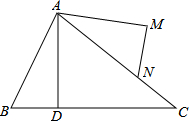 已知:如图,∠BAC=∠DAM,AB=AN,AD=AM,求证:∠B=∠ANM.
已知:如图,∠BAC=∠DAM,AB=AN,AD=AM,求证:∠B=∠ANM.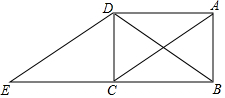 如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.
如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.