Question

18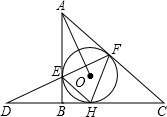．已知直角三角形ABC外切于⊙O，E、F、H为切点，∠ABC=90°，直线FE、CB相交于点D，连接AO、HE、HF，圆O的半径为4．有下列结论：①劣弧EH的长度是π；②∠FEH=30°+∠FAO；③BD=AF；④DH²=AO•DF．其中正确结论的个数为（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 连接OE，OH，OF，OB，
①由切线的性质和四边形的内角和即可判定；
②同①的方法得到∠FOH=180°-∠C=90°+∠BAC，再由圆周角定理即可得到证明；
③根据已知条件知道四边形OEBH是正方形，然后证明△BDE≌△FAO，然后即可题目结论；
④根据已知条件可以证明△DFH∽△ABO，根据相似三角形的对应边成比例和已知条件即可证明结论正确．

解答 解：①中，连接OE，OH，
则OE⊥AB，OH⊥BC，
∵∠ABC=90°，
∴∠EOH=90°，
∵圆O的半径为4，
∴$\widehat{EH}$的长度=$\frac{90•π•4}{180}$=2π，故①错误；
②中，同①的方法得∠FOH=180°-∠C=90°+∠BAC，
根据圆周角定理得∠FEH=$\frac{1}{2}$∠FOH=45°+∠FAO，故②错误；
③中，连接OF，由①得四边形OEBH是正方形，
∴OF=BE，
又∵∠DBE=∠AFO，∠BED=∠AEF=∠AFE=∠AOF，
在△BDE与△FAO中，
$\left\{\begin{array}{l}{∠DBE=∠AFO=90°}\\{BE=OF}\\{∠BED=∠AOF}\end{array}\right.$
∴△BDE≌△FAO，
∴BD=AF，故③正确；
④中，连接OB，
根据两个角对应相等得△DFH∽△ABO，
则DH•AB=AO•DF，
又∵AB=DH，
∴DH²=AO•DF．故④正确．
故选B．

点评 本题考查了切线的性质定理、切线长定理、圆周角定理和相似三角形的性质和判定，熟练掌握定理是解题的关键．