题目内容
 如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α,将△AOC绕顶点C按顺时针方向旋转90°得△BDC,连结OD,
如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α,将△AOC绕顶点C按顺时针方向旋转90°得△BDC,连结OD,(1)当α=95°时,是判断△BOD的形状,并说明理由;
(2)若OC=1,OA=2,OB=
| 2 |
(3)当α等于多少度时,△BOD是等腰三角形?
考点:旋转的性质,等腰三角形的判定,等腰直角三角形
专题:计算题
分析:(1)先根据旋转的性质得∠OCD=90°,CO=CD,∠CDB=∠COA=α,于是可判断△COD是等腰直角三角形,则∠COD=∠CDO=45°,所以∠BOD=360°-∠AOB-∠AOC-∠COD=80°,接着计算出∠BDO=∠CDB-∠CDO=50°,则可根据三角形内角和定理计算出∠DBO=180°-∠BDO-∠BOD=50°,即有∠DBO=∠BDO,于是可判断BOD为等腰三角形;
(2)由△COD是等腰直角三角形得到OD=
OC=
,则OB2+OD2=BD2,根据勾股定理的逆定理得到△BOD为等腰直角三角形,∠BOD=90°;
(3)先分别表示出∠BOD=360°-∠AOB-∠AOC-∠COD=175°-α,∠BDO=∠CDB-∠CDO=α-45°,再计算出∠OBD=180°-∠BDO-∠BOD=50°,然后分类讨论:当OB=OD时,则∠OBD=∠BDO,即α-45°=50°,解得α=95°;当DB=DO时,∠BOD=∠DBO,即175°-α=α-45°,解得α=110°.
(2)由△COD是等腰直角三角形得到OD=
| 2 |
| 2 |
(3)先分别表示出∠BOD=360°-∠AOB-∠AOC-∠COD=175°-α,∠BDO=∠CDB-∠CDO=α-45°,再计算出∠OBD=180°-∠BDO-∠BOD=50°,然后分类讨论:当OB=OD时,则∠OBD=∠BDO,即α-45°=50°,解得α=95°;当DB=DO时,∠BOD=∠DBO,即175°-α=α-45°,解得α=110°.
解答:解:(1)△BOD为等腰三角形. 理由如下:
理由如下:
∵△AOC绕直角顶点C按顺时针方向旋转90°得△BDC,
∴∠OCD=90°,CO=CD,∠CDB=∠COA=α,
∴△COD是等腰直角三角形;
∴∠COD=∠CDO=45°,
∵∠BOD=360°-∠AOB-∠AOC-∠COD
=360°-140°-95°-45°
=80°,
而∠BDO=∠CDB-∠CDO=95°-45°=50°,
∴∠DBO=180°-∠BDO-∠BOD=50°,
∴∠DBO=∠BDO,
∴△BOD为等腰三角形;
(2)∵△COD是等腰直角三角形,
∴OD=
OC=
,
而BD=OA=2,OB=
,
∴OB2+OD2=BD2,
∴△BOD为等腰直角三角形,
∠BOD=90°;
(3)∠BOD=360°-∠AOB-∠AOC-∠COD=360°-140°-α-45°=175°-α,
∠BDO=∠CDB-∠CDO=α-45°,
∠OBD=180°-∠BDO-∠BOD=180°-α+45°-175°+α=50°,
当OB=OD时,∠OBD=∠BDO,即α-45°=50°,解得α=95°;
当DB=DO时,∠BOD=∠DBO,即175°-α=α-45°,解得α=110°,
即当α等于95°或110°时,△BOD是等腰三角形.
 理由如下:
理由如下:∵△AOC绕直角顶点C按顺时针方向旋转90°得△BDC,
∴∠OCD=90°,CO=CD,∠CDB=∠COA=α,
∴△COD是等腰直角三角形;
∴∠COD=∠CDO=45°,
∵∠BOD=360°-∠AOB-∠AOC-∠COD
=360°-140°-95°-45°
=80°,
而∠BDO=∠CDB-∠CDO=95°-45°=50°,
∴∠DBO=180°-∠BDO-∠BOD=50°,
∴∠DBO=∠BDO,
∴△BOD为等腰三角形;
(2)∵△COD是等腰直角三角形,
∴OD=
| 2 |
| 2 |
而BD=OA=2,OB=
| 2 |
∴OB2+OD2=BD2,
∴△BOD为等腰直角三角形,
∠BOD=90°;
(3)∠BOD=360°-∠AOB-∠AOC-∠COD=360°-140°-α-45°=175°-α,
∠BDO=∠CDB-∠CDO=α-45°,
∠OBD=180°-∠BDO-∠BOD=180°-α+45°-175°+α=50°,
当OB=OD时,∠OBD=∠BDO,即α-45°=50°,解得α=95°;
当DB=DO时,∠BOD=∠DBO,即175°-α=α-45°,解得α=110°,
即当α等于95°或110°时,△BOD是等腰三角形.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质、勾股定理的逆定理.

练习册系列答案
相关题目
 在正方形ABCD中,P是AB中点,PQ⊥AC,垂足为Q,求
在正方形ABCD中,P是AB中点,PQ⊥AC,垂足为Q,求 如图,在△ABC中,AB=AC,D,E分别是边BC,AC上的点,且BD=EC,∠ADE=∠B.
如图,在△ABC中,AB=AC,D,E分别是边BC,AC上的点,且BD=EC,∠ADE=∠B.
 如图,以△ABC的AB、AC边为斜边向外作Rt△ABD和Rt△ACE,且使∠ABD=∠ACE,M是BC的中点,求证:DM=ME.
如图,以△ABC的AB、AC边为斜边向外作Rt△ABD和Rt△ACE,且使∠ABD=∠ACE,M是BC的中点,求证:DM=ME.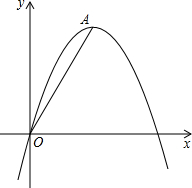 已知:如图,抛物线的解析式为y=-x2+4x.点A为顶点,连结OA,点B是抛物线上另一点.若△AOB是以OA为直角边的直角三角形,求点B的坐标.
已知:如图,抛物线的解析式为y=-x2+4x.点A为顶点,连结OA,点B是抛物线上另一点.若△AOB是以OA为直角边的直角三角形,求点B的坐标.