题目内容
如图,C是线段AB上的一点,且AC比AB的一半还多2cm,D是AB的三等分点,E是CB的中点,DC比CE长1cm,求线段AB的长.


考点:两点间的距离
专题:
分析:根据点之间的关系,可得DC用AB的表示,CE用AB的表示,根据DC与CE的关系,可得关于AB的方程,根据解方程,可得答案.
解答:解:当AD=
AB时,AC比AB的一半还多2cm,得
AC=
AB+2,BC=
AB-2.
由线段的和差,得DC=AC-AD=
AB+2-
AB=
AB+2.
E是CB的中点,得CE=
CB=
AB-1.
由DC比CE长1cm,得
DC-CE=
AB+2-(
AB-1)=1.
-
AB=-2.
解得AB=24,
当AD=
AB时,由线段的和差,得DC=AD-AC=
AB-(
AB+2)=
AB-2,
由DC比CE长1cm,得
DC-CE=
AB-2-(
AB-1)=1.
解得AB=-24(不符合题意,舍);
综上所述:AB=24cm.
| 1 |
| 3 |
AC=
| 1 |
| 2 |
| 1 |
| 2 |
由线段的和差,得DC=AC-AD=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
E是CB的中点,得CE=
| 1 |
| 2 |
| 1 |
| 4 |
由DC比CE长1cm,得
DC-CE=
| 1 |
| 6 |
| 1 |
| 4 |
-
| 1 |
| 12 |
解得AB=24,
当AD=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
由DC比CE长1cm,得
DC-CE=
| 1 |
| 6 |
| 1 |
| 4 |
解得AB=-24(不符合题意,舍);
综上所述:AB=24cm.
点评:本题考查了两点间的距离,利用了线段的和差,分类讨论是解题关键,不符合题意的要舍去.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
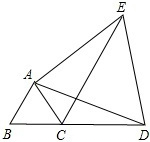 已知,如图,△ABC为等边三角形,D是BC延长线上一点,联结AD,以AD为边作等边三角形ADE,联结CE,用你学过的知识探索AC,CD,CE三条线段之间的数量关系,试写出探究过程.
已知,如图,△ABC为等边三角形,D是BC延长线上一点,联结AD,以AD为边作等边三角形ADE,联结CE,用你学过的知识探索AC,CD,CE三条线段之间的数量关系,试写出探究过程. 如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α,将△AOC绕顶点C按顺时针方向旋转90°得△BDC,连结OD,
如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α,将△AOC绕顶点C按顺时针方向旋转90°得△BDC,连结OD, 如图,将△ABC绕点B旋转到△A1B1C1的位置时,AA1∥BC,∠ABC=80°,则∠CBC1=
如图,将△ABC绕点B旋转到△A1B1C1的位置时,AA1∥BC,∠ABC=80°,则∠CBC1=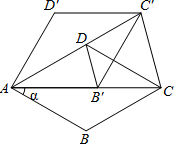 如图,在菱形ABCD中,∠BAD=60°,把菱形ABCD绕点A按逆时针方向旋转α,得到菱形AB′C′D′.问α的度数为多少时,射线AB′经过点C(此时射线AD也经过点C′)?
如图,在菱形ABCD中,∠BAD=60°,把菱形ABCD绕点A按逆时针方向旋转α,得到菱形AB′C′D′.问α的度数为多少时,射线AB′经过点C(此时射线AD也经过点C′)? 如图,方格纸中的每个小正方形的边长均为1,若在图①至图④的位置选一个补画正方形,使所得图案为中心对称图形,则应该选择的是( )
如图,方格纸中的每个小正方形的边长均为1,若在图①至图④的位置选一个补画正方形,使所得图案为中心对称图形,则应该选择的是( ) 如图,AC+BC
如图,AC+BC