题目内容
 如图,以△ABC的AB、AC边为斜边向外作Rt△ABD和Rt△ACE,且使∠ABD=∠ACE,M是BC的中点,求证:DM=ME.
如图,以△ABC的AB、AC边为斜边向外作Rt△ABD和Rt△ACE,且使∠ABD=∠ACE,M是BC的中点,求证:DM=ME.考点:全等三角形的判定与性质
专题:证明题
分析:如图,取AB、AC的中点,连接MP、DP,MQ、EQ,易证DP=MQ,MP=EQ和∠MPD=∠MQE,即可证明△DPM≌△MQE,即可解题.
解答:证明:如图,取AB、AC的中点,连接MP、DP,MQ、EQ,

∵M是BC中点,
∴PM、MQ都是△ABC的中位线,
∴PM∥AC,MQ∥AB,PM=
AC,MQ=
AB,
∵△ABD和△ACE都是直角三角形,
∴DP=
AB,EQ=
AC,
∴DP=MQ,MP=EQ,
∵∠MPD=∠BPD+∠BPM=2∠BAD+∠BAC=2(90°-∠ABD)+∠BAC,
∠MQE=∠CQE+∠CQM=2∠CAE+∠BAC=2(90°-∠ACE)+∠BAC,
∴∠MPD=∠MQE,
在△DPM和△MQE中,
,
∴△DPM≌△MQE(SAS),
∴DM=ME.

∵M是BC中点,
∴PM、MQ都是△ABC的中位线,
∴PM∥AC,MQ∥AB,PM=
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABD和△ACE都是直角三角形,
∴DP=
| 1 |
| 2 |
| 1 |
| 2 |
∴DP=MQ,MP=EQ,
∵∠MPD=∠BPD+∠BPM=2∠BAD+∠BAC=2(90°-∠ABD)+∠BAC,
∠MQE=∠CQE+∠CQM=2∠CAE+∠BAC=2(90°-∠ACE)+∠BAC,
∴∠MPD=∠MQE,
在△DPM和△MQE中,
|
∴△DPM≌△MQE(SAS),
∴DM=ME.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△DPM≌△MQE是解题的关键.

练习册系列答案
相关题目
 如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α,将△AOC绕顶点C按顺时针方向旋转90°得△BDC,连结OD,
如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α,将△AOC绕顶点C按顺时针方向旋转90°得△BDC,连结OD, 如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数y=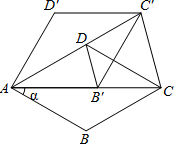 如图,在菱形ABCD中,∠BAD=60°,把菱形ABCD绕点A按逆时针方向旋转α,得到菱形AB′C′D′.问α的度数为多少时,射线AB′经过点C(此时射线AD也经过点C′)?
如图,在菱形ABCD中,∠BAD=60°,把菱形ABCD绕点A按逆时针方向旋转α,得到菱形AB′C′D′.问α的度数为多少时,射线AB′经过点C(此时射线AD也经过点C′)?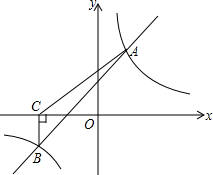 如图,一次函数y=kx+b(k≠0)与反比例函数y=
如图,一次函数y=kx+b(k≠0)与反比例函数y= 如图,在平面直角坐标系中,点A(-5,0),以OA为半径作半圆,点C是第一象限内圆周上一动点,连结AC、BC,并延长BC至点D,使CD=BC,过点D作x轴垂线,分别交x轴、直线AC于点E、F,点E为垂足,连结OF.
如图,在平面直角坐标系中,点A(-5,0),以OA为半径作半圆,点C是第一象限内圆周上一动点,连结AC、BC,并延长BC至点D,使CD=BC,过点D作x轴垂线,分别交x轴、直线AC于点E、F,点E为垂足,连结OF.