题目内容
 在正方形ABCD中,P是AB中点,PQ⊥AC,垂足为Q,求
在正方形ABCD中,P是AB中点,PQ⊥AC,垂足为Q,求| PQ |
| AB |
| PQ |
| AC |
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:如图,证明∠B=90°,∠QAP=45°,AB=BC=2AP(设AP为λ);求出AC=2
λ;进而求得PQ=
λ,问题即可解决.
| 2 |
| ||
| 2 |
解答: 解:∵四边形ABCD是正方形,且P是AB中点,
解:∵四边形ABCD是正方形,且P是AB中点,
∴∠B=90°,∠QAP=45°,AB=BC=2AP(设AP为λ);
由勾股定理得:AC2=4λ2+4λ2,
∴AC=2
λ;
∵PQ⊥AC,
∴sin∠QAP=
,
∴PQ=
λ
∴
=
=
,
=
=
.
 解:∵四边形ABCD是正方形,且P是AB中点,
解:∵四边形ABCD是正方形,且P是AB中点,∴∠B=90°,∠QAP=45°,AB=BC=2AP(设AP为λ);
由勾股定理得:AC2=4λ2+4λ2,
∴AC=2
| 2 |
∵PQ⊥AC,
∴sin∠QAP=
| PQ |
| AP |
∴PQ=
| ||
| 2 |
∴
| PQ |
| AB |
| ||||
| 2λ |
| ||
| 4 |
| PQ |
| AC |
| ||||
2
|
| 1 |
| 4 |
点评:该题主要考查了正方形的性质、直角三角形的边角关系及其应用问题;解题的关键是灵活运用正方形的性质来分析、判断、推理或解答.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
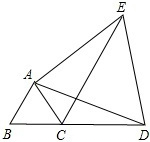 已知,如图,△ABC为等边三角形,D是BC延长线上一点,联结AD,以AD为边作等边三角形ADE,联结CE,用你学过的知识探索AC,CD,CE三条线段之间的数量关系,试写出探究过程.
已知,如图,△ABC为等边三角形,D是BC延长线上一点,联结AD,以AD为边作等边三角形ADE,联结CE,用你学过的知识探索AC,CD,CE三条线段之间的数量关系,试写出探究过程. 如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α,将△AOC绕顶点C按顺时针方向旋转90°得△BDC,连结OD,
如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α,将△AOC绕顶点C按顺时针方向旋转90°得△BDC,连结OD,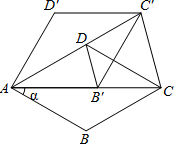 如图,在菱形ABCD中,∠BAD=60°,把菱形ABCD绕点A按逆时针方向旋转α,得到菱形AB′C′D′.问α的度数为多少时,射线AB′经过点C(此时射线AD也经过点C′)?
如图,在菱形ABCD中,∠BAD=60°,把菱形ABCD绕点A按逆时针方向旋转α,得到菱形AB′C′D′.问α的度数为多少时,射线AB′经过点C(此时射线AD也经过点C′)?