题目内容
20.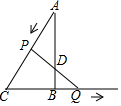 如图,在△ABC中∠ABC=90°,∠A=30°,BC=2cm,动点P以3cm/s的速度由A沿射线AC方向运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交直线AB于D,则当运动时间为$\frac{1}{2}$或3或$\frac{5\sqrt{3}+3}{11}$s时,△ADP是等腰三角形.
如图,在△ABC中∠ABC=90°,∠A=30°,BC=2cm,动点P以3cm/s的速度由A沿射线AC方向运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交直线AB于D,则当运动时间为$\frac{1}{2}$或3或$\frac{5\sqrt{3}+3}{11}$s时,△ADP是等腰三角形.
分析 由∠ABC=90°、∠A=30°、BC=2cm得AC=4cm、AB=ACcosA=2$\sqrt{3}$cm,设运动时间为t,则AP=3t、BQ=t,分以下三种情况:①当PA=PD时,由∠BDQ=∠PDA=∠A=30°知∠C=∠CPQ=60°、DQ=2BQ=2t,得PQ=PC=AC-AP=4-3t,PD=PQ-DQ=4-3t-2t=4-5t,即可知4-5t=3t,解之得出t的值;②当AP=AD时,得∠ADP=∠BDQ=$\frac{180°-∠A}{2}$=75°、∠DQB=15°,以DQ为边在∠BDQ内部作∠EDQ=∠DQB=15°,设DE=QE=x,知∠DEB=30°,可得BE=BQ-EQ=t-x,由cos∠DEB=$\frac{BE}{DE}$可得x=2(2-$\sqrt{3}$)t,根据BD=DEsin∠DEB=(2-$\sqrt{3}$)t知AD=AB-BD=2$\sqrt{3}$-(2-$\sqrt{3}$)t,由AP=AD可得t的值;③当DA=DP时,知∠A=∠APD=30°,从而得∠CQP=∠ACB-∠APD=30°、∠CQP=∠APD=30°,根据CP=CQ可得t的值.
解答 解:∵∠ABC=90°,∠A=30°,BC=2cm,
∴AC=2BC=4cm,AB=ACcosA=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$cm,
设运动时间为t,则AP=3t,BQ=t,
①当PA=PD时,如图1,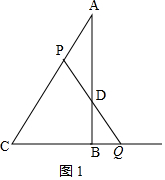
则∠BDQ=∠PDA=∠A=30°,
∴∠C=∠CPQ=60°,DQ=2BQ=2t,
∴PQ=PC=AC-AP=4-3t,
∴PD=PQ-DQ=4-3t-2t=4-5t,
则4-5t=3t,
解得:t=$\frac{1}{2}$;
②当AP=AD时,如图2,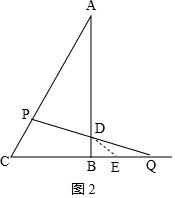
则∠ADP=∠BDQ=$\frac{180°-∠A}{2}$=75°,
∴∠DQB=15°,
以DQ为边在∠BDQ内部作∠EDQ=∠DQB=15°,
∴设DE=QE=x,∠DEB=30°,
∴BE=BQ-EQ=t-x,
由cos∠DEB=$\frac{BE}{DE}$得$\frac{t-x}{x}=\frac{\sqrt{3}}{2}$,
解得:x=2(2-$\sqrt{3}$)t,即DE=2(2-$\sqrt{3}$)t,
∴BD=DEsin∠DEB=(2-$\sqrt{3}$)t,
∴AD=AB-BD=2$\sqrt{3}$-(2-$\sqrt{3}$)t,
由AP=AD得3t=2$\sqrt{3}$-(2-$\sqrt{3}$)t,
解得:t=$\frac{5\sqrt{3}+3}{11}$;
③当DA=DP时,如图3,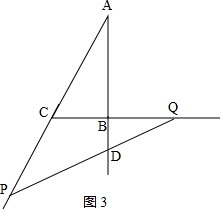
则∠A=∠APD=30°,
∴∠CQP=∠ACB-∠APD=30°,
∴∠CQP=∠APD=30°,
∴CP=CQ,则3t-4=2+t,
解得:t=3,
综上,当运动时间为$\frac{1}{2}$或3或$\frac{5\sqrt{3}+3}{11}$s时,△ADP是等腰三角形.
点评 本题主要考查等腰三角形的判定与性质、解直角三角形的应用及解方程的能力,根据等腰三角形的判定与性质分类讨论,并用t表示出相等的边是解题的关键.

| A. | 角平分线 | B. | 高 | C. | 中线 | D. | 以上都不对 |
| A. | 20° | B. | 40°或140° | C. | 40° | D. | 20°或160° |
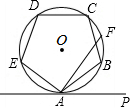 如图,正五边形ABCDE内接于⊙O点F为$\widehat{BC}$的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
如图,正五边形ABCDE内接于⊙O点F为$\widehat{BC}$的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )| A. | 36° | B. | 54° | C. | 60° | D. | 72° |
| A. | 7 | B. | 4 | C. | 1 | D. | 不能确定 |
| A. | 2或16 | B. | -2或-16 | C. | ±2 | D. | ±16 |