题目内容
5.一艘轮船以20km/h的速度离开港口向东北方向航行,另一艘轮船同时离开港口以30km/h的速度向东南方向航行,它们离开港口半小时后相距5$\sqrt{13}$km.分析 根据题意,画出图形,且东北和东南的夹角为90°,根据题目中给出的半小时后和速度可以计算AC,BC的长度,在直角△ABC中,已知AC,BC可以求得AB的长.
解答  解:如图所示:因为东北和东南的夹角为90°,所以△ABC为直角三角形.
解:如图所示:因为东北和东南的夹角为90°,所以△ABC为直角三角形.
在Rt△ABC中,AC=20×0.5=10(km),
BC=30×0.5=15(km),
则AB=$\sqrt{1{0}^{2}+1{5}^{2}}$=5$\sqrt{13}$(km).
故答案为:5$\sqrt{13}$.
点评 本题考查了勾股定理在实际生活中的应用,本题中确定△ABC为直角三角形,并且根据勾股定理计算AB是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知点M(a,3),点N(2,b)关于y轴对称,则(a+b)2015的值( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
13.巴黎与北京的时差为-7小时(正数表示同一时刻比北京时间早的时数),如果北京时间11月11日14:00,那么巴黎时间是( )
| A. | 11月11日21时 | B. | 11月11日7时 | C. | 11月10日7时 | D. | 11月11日5时 |
10.一个两位数的个位数字为a,十位数字比个位数字的2倍少1,若把这个两位数十位上的数字与个位上的数字交换位置组成一个新两位数,则原两位数与新两位数的差为( )
| A. | 9-9a | B. | 11a-11 | C. | 9a-9 | D. | 33a-11 |
14.一个正数的两个平方根分别是2a-1与-a+2,则a的值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
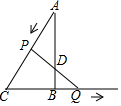 如图,在△ABC中∠ABC=90°,∠A=30°,BC=2cm,动点P以3cm/s的速度由A沿射线AC方向运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交直线AB于D,则当运动时间为$\frac{1}{2}$或3或$\frac{5\sqrt{3}+3}{11}$s时,△ADP是等腰三角形.
如图,在△ABC中∠ABC=90°,∠A=30°,BC=2cm,动点P以3cm/s的速度由A沿射线AC方向运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交直线AB于D,则当运动时间为$\frac{1}{2}$或3或$\frac{5\sqrt{3}+3}{11}$s时,△ADP是等腰三角形.