题目内容
如图，点O在直线AB上，射线OC平分∠DOB．若∠COB=35°，则∠AOD等于( ).
A. 35° B. 70°
C. 110° D. 145°
C
【解析】∵OC平分∠DOB，∠COB=35°，
∴∠BOD=2∠COB=2×35°=70°,
∴∠AOD=180°-70°=110°.
故选D.
口算题天天练系列答案如图，沿AC方向开山修路，为了加快施工进度，要在山的另一边同时施工，工人师傅在AC上取一点B，在小山外取一点D，连接BD，并延长使DF=BD，过F点作AB的平行线段MF，连接MD，并延长，在其延长线上取一点E，使DE=DM，在E点开工就能使A、C、E成一条直线，你知道其中的道理吗？
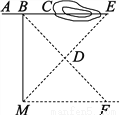
说明见解析
【解析】试题分析：首先证明≌，可得进而得到BE∥MF，再由∥MF根据过直线外一点有且只有一条直线与已知直线平行，可得A、C、E三点在一条直线上．
试题解析：
≌
∴BE∥MF，
∵AB∥MF，
根据过直线外一点有且只有一条直线与已知直线平行，
在一条直线上． 下列四种说法：① x＝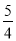
是不等式4x－5＞0的解；② x＝
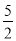是不等式4x－5＞0的一个解；③ x＞
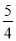是不等式4x－5＞0的解集；④ x＞2中任何一个数都可以使不等式4x－5＞0成立，所以x＞2也是它的解集，其中正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①当 x＝时，不等式4x－5=0，故原命题错误；② 当x＝时，不等式4x－5=5＞0，故原命题正确；③解不等式4x－5＞0得，x＞，故原命题正确；④ 与③矛盾，故错误.故正确的有②和③，故选B. 已知三边作三角形,用到的基本作图是( )
A. 作一个角等于已知角 B. 作已知直线的垂线
C. 作一条线段等于已知线段 D. 作一条线段等于已知线段的和
C
【解析】已知三角形的三边,求作符合要求的三角形,其作图依据是“SSS”.故用到的基本作图是：作一条线段等于已知线段.
故选C. 如图所示，直线AB与CD相交于点O，OE平分∠AOD，∠BOC=80°，求∠BOD和∠AOE的度数.
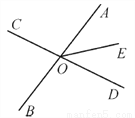
∠AOE=40°.
【解析】试题分析: 根据∠BOD与∠BOC是邻补角,∠BOC=80°,可求得:∠BOD=180°—∠BOC=100°,再根据∠AOD与∠BOC是对顶角,可得:∠AOD=∠BOC=80°,因为OE平分∠AOD,所以∠AOE=∠BOC=40°.
试题解析:因为∠BOD与∠BOC是邻补角,∠BOC=80°,
所以∠BOD=180°—∠BOC=100°,
又因为... 下面四个图形中，∠1=∠2一定成立的是( )
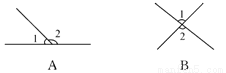
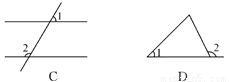
A. （A） B. （B） C. （C） D. （D）
B
【解析】A选项,∠1和∠2是邻补角,∠1+∠2=180°,故本选项错误,
B选项,∠1和∠2是对顶角,根据其定义,故本选项正确,
C选项,根据平行线的性质:同位角相等,同旁内角互补,内错角相等,故本选项错误,
D选项,根据三角形的外角一定大于与它不相邻的内角，故本选项错误,
故选B． 如图，直线AB和CD相交于点O，则∠AOC的邻补角是__________.
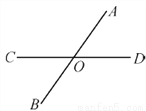
∠AOD和∠BOC
【解析】因为AB和CD交于点O,则∠AOC的邻补角是∠AOD和∠BOC,故答案为: ∠AOD和∠BOC. 用计算器求下列各式的值：
（1）sin47°；
（2）sin12°30′；
（3）cos25°18′；
（4）tan44°59′59″；
（5）sin18°+cos55°-tan59°
（1）0.7314；（2）0.2164；（3）0.9003；（4）1.0000；（5）0.7817
【解析】试题分析：把度、分、秒统一为度，然后利用计算器进行计算即可．最后结果利用四舍五入法取小数点后四位．
试题解析：
解：根据题意用计算器求出：
（1）sin47°=0.7314；
（2）sin12°30′=0.2164；
（3）cos25°18′=0.9003... 下列事件为必然事件的是( )
A. 任意买一张电影票,座位号是奇数
B. 两边及其夹角对应相等的两个三角形全等
C. 打开电视机,正在播放纪录片
D. 三根长度为4 cm,4 cm,8 cm的木棒能摆成三角形
B
【解析】解：A、任意买一张电影票，座位号是奇数，是随机事件，选项错误；
B、两边及其夹角对应相等的两个三角形全等，是必然事件，选项正确；
C、打开电视机，正在播放纪录片，是随机事件，选项错误；
D、三根长度为4cm，4cm，8cm的木棒能摆成三角形，是不可能事件，选项错误．
故选B．