题目内容
17.一个多边形的内角和是1260°,这个多边形的边数是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 设边数为n,由多边形内角和公式可列方程,可求得边数.
解答 解:
设这个多边形的边数为n,
由题意可得:(n-2)×180°=1260°,
解得n=9,
∴这个多边形的边数为9,
故选D.
点评 本题主要考查多边形的内角和,掌握多边形的内角和公式是解题的关键,即多边形的内角和=(n-2)180°.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
7.某工厂生产某种型号的配件,为保证质量,有些不合格的配件不能出厂,因此会使得每天的产量有所不同.表是某周的生产情况:(以日平均生产2000个为标准,超过为正,不足为负,每周按五个工作日生产.)
(1)根据记录可知这一周第一天生产2010 个配件;
(2)这一周产量最多的一天比产量最少的一天多生产42个配件;
(3)已知这种型号的配件每个的产值为15元.请你以该周产量估计该工厂生产这种型号的配件的年产值是多少元.(一年按52周计算,结果用科学计数法表示.)
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 增减 | +10 | -4 | -8 | +22 | -20 |
(2)这一周产量最多的一天比产量最少的一天多生产42个配件;
(3)已知这种型号的配件每个的产值为15元.请你以该周产量估计该工厂生产这种型号的配件的年产值是多少元.(一年按52周计算,结果用科学计数法表示.)
5.反比例函数y=$\frac{6}{x}$图象上有三个点(-2,y1),(-1,y2),(1,y3),则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y1<y2 | C. | y2<y1<y3 | D. | y3<y2<y1 |
2.抛物线y=ax2+bx+c(a≠0)过(2,8)和(-6,8)两点,则此抛物线的对称轴为( )
| A. | 直线x=0 | B. | 直线x=1 | C. | 直线x=-2 | D. | 直线x=-1 |
 圆锥的母线与高的夹角为30°,母线长为6cm,求它的侧面积.
圆锥的母线与高的夹角为30°,母线长为6cm,求它的侧面积.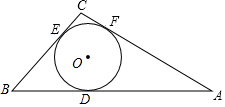 如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于点D、E、F,则AF的长为4.5.
如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于点D、E、F,则AF的长为4.5. 已知:两条定直线a,b在直线a上有一个定点A,在直线a上求一点B,在直线b上求一点P,使两点A、B与点P的连线总长最短.
已知:两条定直线a,b在直线a上有一个定点A,在直线a上求一点B,在直线b上求一点P,使两点A、B与点P的连线总长最短.