Question

已知正方形ABCD的边长为4，点E在BC上，CE=1，线段MN在对角线AC上．MN=

2

，连BM，EN．

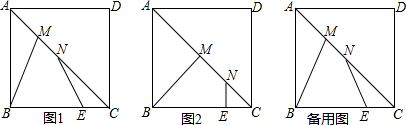
（1）如图1，当点N是AC的中点时，求BM+EN的值；
（2）如图2，当点M是AC的中点时，求BM+EN的值；
（3）当线段MN在对角线AC上运动时，BM+EN的最小值为

 

．

Answer 1

考点：四边形综合题

专题：综合题

分析：（1）连接BN，过N作NH垂直于BC，根据正方形ABCD得到三角形ANB与三角形BHN都为等腰直角三角形，求出BN与NH的长，在直角三角形BNM中，利用勾股定理求出BM的长，在直角三角形NHE中，利用勾股定理求出EN的长，即可确定出BM+EN的长；
（2）由正方形ABCD，M为AC的中点，求出BM，AM，CM的长，根据CM-MN求出CN的长，若过N作NE′⊥BC于点E′，则得到NE′=CE′=1，即E′与E重合，此时NE=NE′=1，即可确定出BM+EN的长；
（3）ME+EN的最小值为

13

，理由为：作出点E关于AC的对称点E′，则CE′=CE=1，将MN平移至E′F处，则四边形MNE′F为平行四边形，连接BF，EF，过F作FG⊥CD于G，可得△E′FG为等腰直角三角形，进而得到E′F=MN，FG=E′G，即四边形EFGC为矩形，求出EF与BE长，利用勾股定理求出BF的长，在三角形BMF中，利用两边之和大于第三边求出BM+EN的最小值即可．

解答：解：（1）连接BN，过N作NH⊥BC于H，如图1所示，

∵正方形ABCD，N为AC中点，
∴△ANB与△BHN都为等腰直角三角形，
∴AN=BN=

2

2

AB=2

2

，NH=CH=

2

2

BN=2，
在Rt△BNM中，由勾股定理得：BM=

BN2+MN2

=

(2 2 )2+( 2 )2

=

10

，
在Rt△NHE中，NH=2，HE=2-1=1，EN=

NH2+HE2

=

5

，
则BM+EN=

10

+

5

；
（2）∵正方形ABCD，M为AC中点，
∴BM=AM=CM=2

2

，
∵MN=

2

，
∴CN=CM-MN=

2

，
若过N作NE′⊥BC于点E′，如图2所示，则得到NE′=CE′=1，

∴E′与E重合，且NE=NE′=1，
∴BM+EN=2

2

+1；
（3）ME+EN的最小值为

13

，理由为：
如图3所示，作出点E关于AC的对称点E′，则CE′=CE=1，
将MN平移至E′F处，则四边形MNE′F为平行四边形，
连接BF，EF，过F作FG⊥CD于G，可得△E′FG为等腰直角三角形，

∴E′F=MN=

2

，FG=E′G=1=CE，
∴四边形CEFG为矩形，
∴EF=CG=2，BE=BC-CE=3，
∴BF=

BE2+EF2

=

13

，
显然，BM+EN=BM+E′N=BM+FM≥BF=

13

．

点评：此题属于四边形综合题，涉及的知识有：正方形的性质，等腰直角三角形的性质，勾股定理，平移的性质，平行四边形的性质，熟练掌握性质及定理是解本题的关键．