题目内容
17.(1)计算:-12016-32÷(-3)+(-$\frac{1}{2}$)0•sin60°-$\sqrt{27}$;(2)已知关于x的方程$\frac{2}{x-2}+\frac{x+m}{2-x}$=2有增根,求m的值.
分析 (1)原式利用乘方的意义,零指数幂法则,特殊角的三角函数值,以及二次根式性质计算即可得到结果;
(2)分式方程去分母转化为整式方程,由分式方程有增根,求出x的值,确定出m的值即可.
解答 解:(1)原式=-1+3+$\frac{\sqrt{3}}{2}$-3$\sqrt{3}$=2-$\frac{5\sqrt{3}}{2}$;
(2)去分母得:2-x-m=2x-4,
由分式方程有增根,得到x-2=0,即x=2,
把x=2代入整式方程得:-m=0,
解得:m=0.
点评 此题考查了实数的运算,以及分式方程的增根,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
8.下图是上海今年春节七天最高气温(℃)的统计结果:
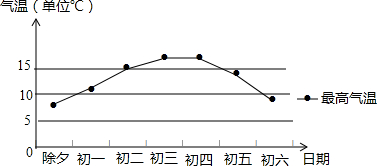
这七天最高气温的众数和中位数是( )

这七天最高气温的众数和中位数是( )
| A. | 15,17 | B. | 14,17 | C. | 17,14 | D. | 17,15 |
5.截止到目前,参加北京市普通小客车摇号的申请人数已经超过2500000人,将2500000用科学记数法表示为( )
| A. | 25×10 5 | B. | 2.5×106 | C. | 0.25×10 7 | D. | 2.5×108 |
6.不等式组$\left\{\begin{array}{l}{x+1>0}\\{\frac{x}{3}<\frac{x+1}{4}}\end{array}\right.$的解集是( )
| A. | -1<x<3 | B. | -1≤x<1 | C. | x<3 | D. | x≥-1 |
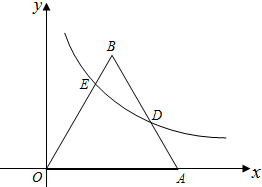 如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.
如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.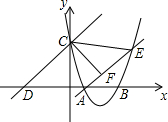 如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.
如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.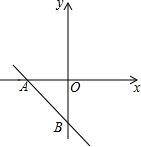 如图,在平面直角坐标系中,一次函数y=-x-3分别与x轴、y轴相交于A、B两点,二次函数y=x2+mx+n(m≠6)的图象经过点A.
如图,在平面直角坐标系中,一次函数y=-x-3分别与x轴、y轴相交于A、B两点,二次函数y=x2+mx+n(m≠6)的图象经过点A.