题目内容
7．
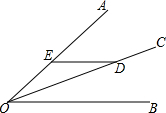如图，D是∠AOB平分线OC上一点，过点D作DE∥OB交射线OA于点E，已知∠BOD=25°，则∠OED=（ ）| A． | 40° | B． | 50° | C． | 130° | D． | 150° |
分析 首先由平行线的性质求得∠EDO=∠DOB=25°，然后根据角平分线的定义求得∠EOD=∠DOB=25°，最后根据三角形的内角和定理即可求得∠CED的度数．
解答 解：∵ED∥OB，
∴∠EDO=∠DOB=25°．
∵D是∠AOB平分线OC上一点，
∴∠EOD=∠COB=25°
∠OED=180°-∠EOD-∠EDO=180°-25°-25°=130°．
点评 本题主要考查的是平行线的性质、角平分线的定义以及三角形的内角和定理，根据平行线的性质和角平分线的定义求得∠EOD、∠EDO的度数是解题的关键．
练习册系列答案
相关题目
△COD是△AOB绕点O顺时针方向旋转40°后所得的图形，点C恰好在AB上，∠AOD=95°，则∠D的度数是55°．
12．
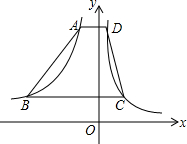如图，在横跨第一、二象限的梯形ABCD中，AD∥BC∥x轴，AD=1，BC=4，它的高为4，四个顶点都在反比例函数的图象上，则关于A，B两点坐标说法错误的是（ ）
如图，在横跨第一、二象限的梯形ABCD中，AD∥BC∥x轴，AD=1，BC=4，它的高为4，四个顶点都在反比例函数的图象上，则关于A，B两点坐标说法错误的是（ ）| A． | A点的横坐标是-$\frac{3}{5}$，B点的横坐标是-3 | |
| B． | A点的横坐标是-$\frac{3}{5}$，B点的纵坐标是$\frac{4}{3}$ | |
| C． | A点的纵坐标是$\frac{16}{3}$，B点的横坐标是-3 | |
| D． | A点的纵坐标是$\frac{16}{3}$，B点的纵坐标是$\frac{4}{3}$ |
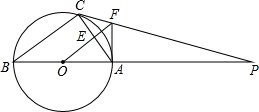如图，△ABC内接于⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于点E，交PC于点F，连接AF；