题目内容
18.一个圆锥的侧面展开图是半径为8cm、圆心角为120°的扇形,则此圆锥底面圆的半径为$\frac{8}{3}$cm.分析 把扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
解答 解:设此圆锥的底面半径为r,
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得,
2πr=$\frac{120π×8}{180}$,
r=$\frac{8}{3}$cm.
故答案为:$\frac{8}{3}$cm.
点评 主要考查了圆锥侧面展开扇形与底面圆之间的关系,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
10.下列计算正确的是( )
| A. | -|-2|=-2 | B. | 20=0 | C. | 2-1-=-2 | D. | $\sqrt{4}$=±2 |
7.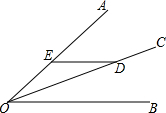 如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )
如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )
 如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )
如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |
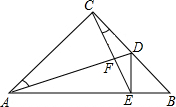 如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD是BC上的中线,CE⊥AD于F,交AB于E,连结DE,问∠CDA与∠BDE相等吗?为什么?
如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD是BC上的中线,CE⊥AD于F,交AB于E,连结DE,问∠CDA与∠BDE相等吗?为什么?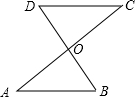 已知:如图,AC和BD相交于点O,OA=OC,OB=OD.
已知:如图,AC和BD相交于点O,OA=OC,OB=OD.