题目内容
2. △COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=95°,则∠D的度数是55°.
△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=95°,则∠D的度数是55°.
分析 先根据旋转的性质得∠AOC=∠BOD=40°,OA=OC,∠OCD=∠A,根据等腰三角形的性质和三角形内角和可计算出∠A=70°,则∠OCD=70°,再由∠AOD=∠AOC+∠COD=95°计算出∠COD=55°,然后在△OCD中利用三角形内角和定理可计算出∠D的度数.
解答 解:∵△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
∴∠AOC=∠BOD=40°,OA=OC,∠OCD=∠A,
∵OA=OC,
∴∠A=∠ACO,
∴∠A=$\frac{1}{2}$(180°-40°)=70°,
∴∠OCD=70°,
∵∠AOD=∠AOC+∠COD=95°,
∴∠COD=95°-40°=55°,
∴∠D=180°-∠COD-∠OCD=180°-55°-70°=55°.
故答案为55°
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质和三角形内角和定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列各式计算正确的是( )
| A. | $\sqrt{3}-\sqrt{2}$=1 | B. | a6÷a2=a3 | C. | x2+x3=x5 | D. | (-x2)3=-x6 |
10.下列计算正确的是( )
| A. | -|-2|=-2 | B. | 20=0 | C. | 2-1-=-2 | D. | $\sqrt{4}$=±2 |
17.为了了解某班学生每天使用零花钱数(单位:元)的情况,小王随机调查了15名同学,结果如下表:
则这15名同学每天使用零花钱的众数和中位数分别是( )
| 每天使用零花钱数 | 1 | 2 | 3 | 5 | 6 |
| 人数 | 2 | 5 | 4 | 3 | 1 |
| A. | 2元、3元 | B. | 2.5元、3元 | C. | 2元、2.5元 | D. | 3元、2.5元 |
7.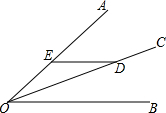 如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )
如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )
 如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )
如图,D是∠AOB平分线OC上一点,过点D作DE∥OB交射线OA于点E,已知∠BOD=25°,则∠OED=( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |
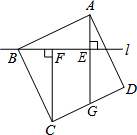 如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.