题目内容
12. 如图,四边形ABCD是平行四边形,点E在CD上,连接AE交BD于点F,则下列结论错误的是( )
如图,四边形ABCD是平行四边形,点E在CD上,连接AE交BD于点F,则下列结论错误的是( )| A. | $\frac{DE}{AB}$=$\frac{DF}{BF}$ | B. | $\frac{AF}{FE}$=$\frac{BF}{FD}$ | C. | $\frac{AF}{AE}$=$\frac{DF}{BD}$ | D. | $\frac{DE}{DC}$=$\frac{EF}{AF}$ |
分析 由四边形ABCD是平行四边形,可得AB∥CD,AB=CD,易证得△ABF∽△EDF,然后由平行线分线段成比例定理与相似三角形的性质,求得答案.
解答 解:四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴$\frac{AF}{FE}=\frac{BF}{FD}$,$\frac{AF}{AE}$=$\frac{BF}{BD}$,故B,
∴△ABF∽△EDF,
∴$\frac{DE}{AB}=\frac{DF}{BF}$,故A正确,
同理:D正确;
∴$\frac{DE}{DC}$=$\frac{EF}{AF}$,故C错误;
故选C.
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质.注意掌握各线段的对应关系是解此题的关键.

练习册系列答案
相关题目
2.下列运算正确的是( )
| A. | a2•a2=a4 | B. | (a-b)2=a2-b2 | C. | 2+$\sqrt{2}$=2$\sqrt{2}$ | D. | (-a3)2=-a6 |
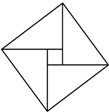 如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )
如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )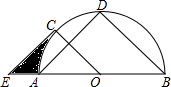 如图所示,AB为半圆O的直径,点D是半圆弧的中点,半径OC∥BD,过点C作AD的平行线交BA延长线于点E.
如图所示,AB为半圆O的直径,点D是半圆弧的中点,半径OC∥BD,过点C作AD的平行线交BA延长线于点E. 已知:⊙O的半径为5,PO=3
已知:⊙O的半径为5,PO=3