题目内容
1．
已知：⊙O的半径为5，PO=3（1）求作：过点P的⊙O的最短弦AB（保留作图痕迹，不写作法）；
（2）求最短弦AB的长．
分析 （1）利用圆内最短的弦为过这点且垂直于这条直径的线段，进而得出答案；
（2）利用垂径定理结合勾股定理得出答案．
解答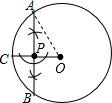 
解：（1）如图所示：线段AB即为所求；
（2）连接AO，
∵⊙O的半径为5，PO=3，
∴AO=$\sqrt{{5}^{2}-{3}^{2}}$=4，
则AB=2×4=8．
点评 本题考查了复杂作图、垂径定理以及勾股定理，注意：圆内最长弦为直径，最短的弦为过这点且垂直于这条直径的线．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
12．
如图，四边形ABCD是平行四边形，点E在CD上，连接AE交BD于点F，则下列结论错误的是（ ）
如图，四边形ABCD是平行四边形，点E在CD上，连接AE交BD于点F，则下列结论错误的是（ ）| A． | $\frac{DE}{AB}$=$\frac{DF}{BF}$ | B． | $\frac{AF}{FE}$=$\frac{BF}{FD}$ | C． | $\frac{AF}{AE}$=$\frac{DF}{BD}$ | D． | $\frac{DE}{DC}$=$\frac{EF}{AF}$ |
9．-$\frac{1}{6}$的倒数的相反数是（ ）
| A． | $\frac{1}{6}$ | B． | 6 | C． | -$\frac{1}{6}$ | D． | -6 |
16．
已知二次函数y=ax2+bx=c（a≠0）的图象如图所示，与y轴相交一点C，与x轴负半轴相交一点A，且OA=OC，有下列5个结论：
①abc＞0；②b＜a+c；③4a+2b+c＞0；④2a+b=0；⑤c+$\frac{1}{a}$=-2．
其中正确的结论有 （ ）
已知二次函数y=ax2+bx=c（a≠0）的图象如图所示，与y轴相交一点C，与x轴负半轴相交一点A，且OA=OC，有下列5个结论：①abc＞0；②b＜a+c；③4a+2b+c＞0；④2a+b=0；⑤c+$\frac{1}{a}$=-2．
其中正确的结论有 （ ）
| A． | ③④⑤ | B． | ③④ | C． | ①②③ | D． | ②③④ |
13．方程3x2-2$\sqrt{6}$x+2=0的根的情况是（ ）
| A． | 无实根 | B． | 有两个等根 | C． | 有两个不等根 | D． | 有分数根 |
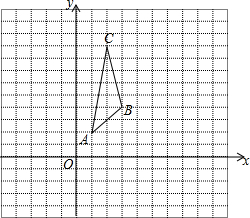在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（1，2），B（3，4），C（2，9）．