题目内容
7.计算下列各式:(1)$\frac{a}{(a-b)(a-c)}$+$\frac{b}{(b-c)(b-a)}$+$\frac{c}{(c-a)(c-b)}$.
(2)$\frac{{a}^{2}-bc}{(a+b)(a+c)}$+$\frac{{b}^{2}-ac}{(b+c)(b+a)}$+$\frac{{c}^{2}-ab}{(c+a)(c+b)}$.
分析 (1)首先把异分母转化成同分母,然后进行加减运算,可得答案;
(2)首先把异分母转化成同分母,然后进行加减运算,可得答案.
解答 解:(1)原式=$\frac{a}{(a-b)(a-c)}$-$\frac{b}{(b-c)(a-b)}$+$\frac{c}{(a-c)(b-c)}$
=$\frac{a(b-c)-b(a-c)+c(a-b)}{(a-b)(a-c)(b-c)}$
=$\frac{ab-ac-ab+ac+ac-ab}{(a-b)(a-c)(b-c)}$
=$\frac{ac-ab}{(a-b)(a-c)(b-c)}$;
(2)原式=$\frac{{(a}^{2}-bc)(b+c)}{(a+b)(a+c)(b+c)}$+$\frac{({b}^{2}-ac)(a+c)}{(a+b)(b+c)(a+c)}$+$\frac{{(c}^{2}-ab)(a+b)}{(a+b)(a+c)(b+c)}$
=-$\frac{ac}{((a+b)(b+c)}$.
点评 本题考查了分式的加减,分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.

练习册系列答案
相关题目
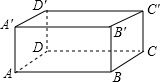 有一个长方形纸盒,长、宽、高分别为4cm、3cm、12cm,请你算一算,能否把一根长为18cm的铅笔放入这个纸盒里面?
有一个长方形纸盒,长、宽、高分别为4cm、3cm、12cm,请你算一算,能否把一根长为18cm的铅笔放入这个纸盒里面?