题目内容
 如图:以△ABC中的AB、AC为边分别向外作正方形ADEB、ACGF,连接DC、BF
如图:以△ABC中的AB、AC为边分别向外作正方形ADEB、ACGF,连接DC、BF(1)观察图形,利用旋转的观点说明:△ADC绕着点
(2)猜想:CD与BF有怎样的数量关系和位置关系?并证明你的猜想.(相关知识链接:正方形的四条边都相等,四个角都是直角)
考点:旋转的性质,全等三角形的判定与性质,正方形的性质
专题:
分析:(1)因为AD=AB,AC=AF,∠DAC=∠BAF=90°+∠BAC,故△ABF可看作△ADC绕A点逆时针旋转90°得到;
(2)要求两条线段的长度关系,把两条线段放到两个三角形中,利用三角形的全等求得两条线段相等;根据全等三角形的对应角相等以及直角三角形的两锐角互补,即可证得∠NMC=90°,可证得证BF⊥CD.
(2)要求两条线段的长度关系,把两条线段放到两个三角形中,利用三角形的全等求得两条线段相等;根据全等三角形的对应角相等以及直角三角形的两锐角互补,即可证得∠NMC=90°,可证得证BF⊥CD.
解答: 解:(1)根据正方形的性质可得:AD=AB,AC=AF,
解:(1)根据正方形的性质可得:AD=AB,AC=AF,
∠DAB=∠CAF=90°,
∴∠DAC=∠BAF=90°+∠BAC,
∴△DAC≌△BAF(SAS),
故△ADC可看作△ABF绕A点逆时针旋转90°得到.
故答案为:A逆时针,90°;
(2)DC=BF,DC⊥BF.
理由:在正方形ABDE中,AD=AB,∠DAB=90°,
又在正方形ACGF,AF=AC,∠FAC=90°,
∴∠DAB=∠FAC=90°,
∵∠DAC=∠DAB+∠BAC,
∠FAB=∠FAC+∠BAC,
∴∠DAC=∠FAB,
在△DAC和△FAB中
∴△DAC≌△FAB(SAS),
∴DC=FB,∠AFN=∠ACD,
又∵在直角△ANF中,∠AFN+∠ANF=90°,∠ANF=∠CNM,
∴∠ACD+∠CNM=90°,
∴∠NMC=90°
∴BF⊥CD,
即CD与BF的数量关系是BF=CD和位置关系是BF⊥CD.
 解:(1)根据正方形的性质可得:AD=AB,AC=AF,
解:(1)根据正方形的性质可得:AD=AB,AC=AF,∠DAB=∠CAF=90°,
∴∠DAC=∠BAF=90°+∠BAC,
∴△DAC≌△BAF(SAS),
故△ADC可看作△ABF绕A点逆时针旋转90°得到.
故答案为:A逆时针,90°;
(2)DC=BF,DC⊥BF.
理由:在正方形ABDE中,AD=AB,∠DAB=90°,
又在正方形ACGF,AF=AC,∠FAC=90°,
∴∠DAB=∠FAC=90°,
∵∠DAC=∠DAB+∠BAC,
∠FAB=∠FAC+∠BAC,
∴∠DAC=∠FAB,
在△DAC和△FAB中
|
∴△DAC≌△FAB(SAS),
∴DC=FB,∠AFN=∠ACD,
又∵在直角△ANF中,∠AFN+∠ANF=90°,∠ANF=∠CNM,
∴∠ACD+∠CNM=90°,
∴∠NMC=90°
∴BF⊥CD,
即CD与BF的数量关系是BF=CD和位置关系是BF⊥CD.
点评:本题考查了旋转的性质,正方形的性质及三角形全等的性质,关键是根据图形中两个三角形的位置关系解题.

练习册系列答案
相关题目
 如图,已知:∠AGD=∠ACB,CD⊥AB于D,EF⊥AB于E,
如图,已知:∠AGD=∠ACB,CD⊥AB于D,EF⊥AB于E,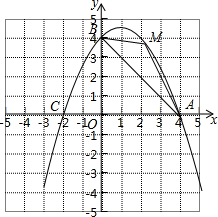 如图,在平面直角坐标系中,已知抛物线经过点A(4,0),B(0,4),C(-2,0)三点.
如图,在平面直角坐标系中,已知抛物线经过点A(4,0),B(0,4),C(-2,0)三点.  已知:如图所示,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,AD平分∠BAC,求证:四边形AEDF是菱形.
已知:如图所示,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,AD平分∠BAC,求证:四边形AEDF是菱形. 尺规作图:
尺规作图: