题目内容
①解方程:x-1=5-(2x+1)
②解方程组:
③解不等式组,并把解集表示在数轴上:
④解方程:2[
x-(
-
)]=
x.
②解方程组:
|
③解不等式组,并把解集表示在数轴上:
|
④解方程:2[
| 4 |
| 3 |
| 2x |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
考点:解一元一次不等式组,解一元一次方程,解二元一次方程组
专题:
分析:①④利用解一元一次方程的方法得出答案即可;
②利用加减消元法求得方程组的解即可;
③首先求得不等式组的解集,再进一步在数轴上表示即可.
②利用加减消元法求得方程组的解即可;
③首先求得不等式组的解集,再进一步在数轴上表示即可.
解答:解:①x-1=5-(2x+1),
x-1=5-2x-1,
x+2x=5-1+1,
3x=5,
x=
;
②
,
(1)+(2)×4得:
11x=22,
x=2,
代入(2)得:
2×2-y=5,
y=-1,
所以方程组的解为
;
③
,
解不等式①得:x≤1,
解不等式②得:x<-4,
所以不等式组的解集为:x<-4,
在数轴上表示为:

④2[
x-(
-
)]=
x,
x-
x+1=
x,
x+1=
x,
16x+12=9x,
7x=-12,
x=-
.
x-1=5-2x-1,
x+2x=5-1+1,
3x=5,
x=
| 5 |
| 3 |
②
|
(1)+(2)×4得:
11x=22,
x=2,
代入(2)得:
2×2-y=5,
y=-1,
所以方程组的解为
|
③
|
解不等式①得:x≤1,
解不等式②得:x<-4,
所以不等式组的解集为:x<-4,
在数轴上表示为:

④2[
| 4 |
| 3 |
| 2x |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 8 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
| 3 |
| 4 |
16x+12=9x,
7x=-12,
x=-
| 12 |
| 7 |
点评:此题考查解一元一次方程,解二元一次方程组,解不等式组的方法与步骤,以及在数轴上表示不等式组的解集的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若△ABC∽△DEF,它们的面积比为4:1,则△ABC与△DEF的对应高的比为( )
| A、2:1 | B、1:2 |
| C、4:1 | D、1:4 |
若9x2+ax+16是完全平方式,则a应是( )
| A、12 | B、-12 |
| C、±12 | D、±24 |
一组数据:3,2,1,2,2的众数,中位数,极差分别是( )
| A、2,1,4 |
| B、2,2,2 |
| C、3,1,2 |
| D、2,1,2 |
 如图,在△ABC中,∠ABC=45°,AB=6,AB的垂直平分线交AC于点E,交BC的延长线于点F,垂足为D,连接AF,则AF的长度是( )
如图,在△ABC中,∠ABC=45°,AB=6,AB的垂直平分线交AC于点E,交BC的延长线于点F,垂足为D,连接AF,则AF的长度是( )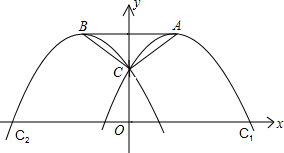 已知抛物线C1:y=-x2+2mx+1(m为常数,且m>0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,连接AC,BC,AB.
已知抛物线C1:y=-x2+2mx+1(m为常数,且m>0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,连接AC,BC,AB. 小丽和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴;若游乐园D的坐标为(1,-2),你能帮她先画出平面直角坐标系,并写出其他各景点的坐标吗?
小丽和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴;若游乐园D的坐标为(1,-2),你能帮她先画出平面直角坐标系,并写出其他各景点的坐标吗? 如图:以△ABC中的AB、AC为边分别向外作正方形ADEB、ACGF,连接DC、BF
如图:以△ABC中的AB、AC为边分别向外作正方形ADEB、ACGF,连接DC、BF