题目内容
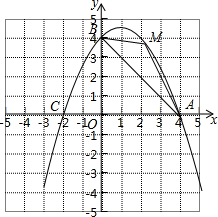 如图,在平面直角坐标系中,已知抛物线经过点A(4,0),B(0,4),C(-2,0)三点.
如图,在平面直角坐标系中,已知抛物线经过点A(4,0),B(0,4),C(-2,0)三点. (1)求抛物线的解析式;
(2)若点M为第一象限内抛物线上的一动点,点M的横坐标为m,△AMB的面积为S,求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的平行四边形,直接写出相应的点Q的坐标.
考点:二次函数综合题
专题:压轴题
分析:(1)设抛物线解析式为y=a(x-4)(x+2),把点B的坐标代入求出a的值,即可得解;
(2)过点M作MN⊥x轴于N,根据△AMB的面积S=S梯形ONMB+S△AMN-S△AOB列式整理即可得到S与m的关系式,然后根据二次函数的最值问题解答;
(3)根据一次函数图象上点的坐标特征,设点Q(x,-x),再分①OB是平行四边形的边,分点P在点Q的上方和下方两种情况表示出点P的坐标,然后根据点P在抛物线上,列出方程求解即可;②OB是平行四边形的对角线时,根据平行四边形的对角线互相平分表示出点P的坐标,然后根据点P在抛物线上,列出方程求解.
(2)过点M作MN⊥x轴于N,根据△AMB的面积S=S梯形ONMB+S△AMN-S△AOB列式整理即可得到S与m的关系式,然后根据二次函数的最值问题解答;
(3)根据一次函数图象上点的坐标特征,设点Q(x,-x),再分①OB是平行四边形的边,分点P在点Q的上方和下方两种情况表示出点P的坐标,然后根据点P在抛物线上,列出方程求解即可;②OB是平行四边形的对角线时,根据平行四边形的对角线互相平分表示出点P的坐标,然后根据点P在抛物线上,列出方程求解.
解答:解:(1)设抛物线解析式为y=a(x-4)(x+2),
把点B(0,4)代入得,-8a=4,
解得a=-
,
所以,抛物线解析式为y=-
(x-4)(x+2),
即y=-
x2+x+4;
(2)∵A(4,0),B(0,4),
∴OA=4,OB=4,
如图,过点M作MN⊥x轴于N,
∵点M的横坐标为m,
∴ON=m,AN=(4-m),MN=-
m2+m+4,
∴△AMB的面积S=S梯形ONMB+S△AMN-S△AOB,
=
(-
m2+m+4+4)×m+
(4-m)(-
m2+m+4)-
×4×4,
=-m2+4m,
∴S关于m的函数关系式为:S=-m2+4m,
∵S=-m2+4m=-(m-2)2+4,
∴当m=2时,S有最大值为4;
(3)∵点Q是直线y=-x上的动点,
∴设点Q(x,-x),
①OB是平行四边形的边时,若点P在点Q的上方,则点P的坐标为(x,-x+4),
∵点P在抛物线y=-
x2+x+4上,
∴-
x2+x+4=-x+4,
整理得,x2-4x=0,
解得x1=0(舍去),x2=4,
此时,点Q的坐标为(4,-4),
若点P在点Q的下方时,则点P的坐标为(x,-x-4),
∵点P在抛物线y=-
x2+x+4上,
∴-
x2+x+4=-x-4,
整理得,x2-4x-16=0,
解得x1=2+2
,x2=2-2
,
此时,点Q的坐标为(2+2
,-2-2
)或(2-2
,-2+2
);
②OB是平行四边形的对角线时,平行四边形对角线的交点为(0,2),
所以,点P的坐标为(-x,x+4),
∵点P在抛物线y=-
x2+x+4上,
∴-
x2-x+4=x+4,
整理得,x2+4x=0,
解得x1=0(舍去),x2=-4,
此时,点Q的坐标为(-4,4),
综上所述,点Q的坐标为(4,-4)或(2+2
,-2-2
)或(2-2
,-2+2
)或(-4,4)时,以点P、Q、B、O为顶点的四边形是平行四边形.
把点B(0,4)代入得,-8a=4,
解得a=-
| 1 |
| 2 |
所以,抛物线解析式为y=-
| 1 |
| 2 |
即y=-
| 1 |
| 2 |
(2)∵A(4,0),B(0,4),
∴OA=4,OB=4,

如图,过点M作MN⊥x轴于N,
∵点M的横坐标为m,
∴ON=m,AN=(4-m),MN=-
| 1 |
| 2 |
∴△AMB的面积S=S梯形ONMB+S△AMN-S△AOB,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-m2+4m,
∴S关于m的函数关系式为:S=-m2+4m,
∵S=-m2+4m=-(m-2)2+4,
∴当m=2时,S有最大值为4;
(3)∵点Q是直线y=-x上的动点,
∴设点Q(x,-x),
①OB是平行四边形的边时,若点P在点Q的上方,则点P的坐标为(x,-x+4),
∵点P在抛物线y=-
| 1 |
| 2 |
∴-
| 1 |
| 2 |
整理得,x2-4x=0,
解得x1=0(舍去),x2=4,
此时,点Q的坐标为(4,-4),
若点P在点Q的下方时,则点P的坐标为(x,-x-4),
∵点P在抛物线y=-
| 1 |
| 2 |
∴-
| 1 |
| 2 |
整理得,x2-4x-16=0,
解得x1=2+2
| 5 |
| 5 |
此时,点Q的坐标为(2+2
| 5 |
| 5 |
| 5 |
| 5 |
②OB是平行四边形的对角线时,平行四边形对角线的交点为(0,2),
所以,点P的坐标为(-x,x+4),
∵点P在抛物线y=-
| 1 |
| 2 |
∴-
| 1 |
| 2 |
整理得,x2+4x=0,
解得x1=0(舍去),x2=-4,
此时,点Q的坐标为(-4,4),
综上所述,点Q的坐标为(4,-4)或(2+2
| 5 |
| 5 |
| 5 |
| 5 |
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,不规则图形的面积的求解,平行四边形的性质,(1)利用抛物线交点式形式更简便,(2)把不规则图形转化为规则的四边形和三角形是解题的关键,(3)难点在于分情况讨论.

练习册系列答案
相关题目
若点O为?ABCD的对角线AC与BD的交点,且AO+BO=10cm,则AC+BD的长是( )
| A、5cm | B、10cm |
| C、20cm | D、40cm |
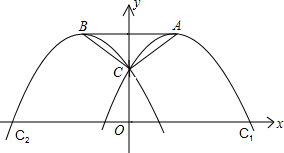 已知抛物线C1:y=-x2+2mx+1(m为常数,且m>0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,连接AC,BC,AB.
已知抛物线C1:y=-x2+2mx+1(m为常数,且m>0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,连接AC,BC,AB. 如图:以△ABC中的AB、AC为边分别向外作正方形ADEB、ACGF,连接DC、BF
如图:以△ABC中的AB、AC为边分别向外作正方形ADEB、ACGF,连接DC、BF 如图,四边形ABCD中,AB∥CD,CE∥AD交AB于E,AE=AD.
如图,四边形ABCD中,AB∥CD,CE∥AD交AB于E,AE=AD.