题目内容
7.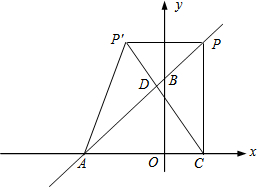 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-6,0),点B的坐标是(0,n)(n>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P′(点P′不在y轴上),连接PP′,P′A,P′C.设点P的横坐标为m.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-6,0),点B的坐标是(0,n)(n>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P′(点P′不在y轴上),连接PP′,P′A,P′C.设点P的横坐标为m.(1)若点P在第一象限,记直线AB与P′C的交点为D.当P′D:DC=2:5时,求m的值;
(2)若点P在第一象限,是否同时存在m,n,使△P′CA为等腰直角三角形?若存在,请求出所有满足要求的m,n的值;若不存在,请说明理由.
分析 (1)由条件可得△P′PD∽△CAD,利用相似三角形的性质可得到关于m的方程,可求得m的值;
(2)分∠AP′C、∠P′AC和∠P′CA分别为直角进行讨论,由等腰三角形可先求得m的值,再根据相似三角形可得到关于n的方程,可求得n的值.
解答 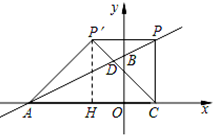 解:
解:
(1)∵PP′∥AC,
∴△P′PD∽△CAD,
∴$\frac{P′P}{AC}$=$\frac{P′D}{DC}$=$\frac{2}{5}$,
∴$\frac{2m}{m+6}$=$\frac{2}{5}$,
解得m=$\frac{3}{2}$;
(2)当点P在第一象限且△P′CA为等腰直角三角形时,分∠AP′C、∠P′AC和∠P′CA分别为直角进行讨论.
第一种情况:
若∠AP′C=90°,P′A=P′C,
过点P′作P′H⊥x轴于点H.
∴PP′=CH=AH=P′H=$\frac{1}{2}$AC.
∴2m=$\frac{1}{2}$(m+6),
∴m=2,P′H=4,
∵△AOB∽△ACP,
∴$\frac{6}{n}$=$\frac{8}{4}$,
∴n=3;
第二种情况:
若∠P′AC=90°,P′A=AC,则PP′=AC,
∴2m=m+6,
∴m=6,
∵△P′AC为等腰直角三角形,
∴四边形P′ACP为正方形,
∴PC=AC=12,
∵△AOB∽△ACP,
∴$\frac{AO}{AC}$=$\frac{OB}{PC}$,即$\frac{6}{12}$=$\frac{n}{12}$,
∴n=6;
第三种情况:
若∠P′CA=90°,则点P′,P都在第一象限内,这与条件矛盾.
∴△P′CA不可能是以C为直角顶点的等腰直角三角形.
∴所有满足条件的m=2,n=3或m=6,n=6.
点评 本题主要考查相似三角形的判定和性质及等腰直角三角形的性质、坐标与图形等知识点的综合应用,在(1)中由条件证明三角形相似,利用相似三角形对应边成比例得到关于m的方程是解题的关键;在(2)中分三种情况分别讨论是解题的关键;属于基础知识的综合考查,难度不大,注意对基础知识的熟练应用.

| A. | $\sqrt{5}$+$\sqrt{7}$=$\sqrt{12}$ | B. | 5+$\sqrt{2}$=5$\sqrt{2}$ | C. | $\sqrt{3}$×$\sqrt{6}$=3$\sqrt{2}$ | D. | $\sqrt{{(-2)}^{2}}$=-2 |
| A. | $\frac{75}{100}$x-20=$\frac{9}{10}$x+25 | B. | $\frac{75}{100}$x+25=$\frac{9}{10}$x-20 | ||
| C. | $\frac{75}{100}$x-25=$\frac{9}{10}$x+20 | D. | $\frac{75}{100}$x+20=$\frac{9}{10}$x+25 |
 在等腰直角△ABC中,∠ACB=90°,D是AC中点,∠ADF=∠CDB,连接CF交BD于E,求证:BD⊥CF.
在等腰直角△ABC中,∠ACB=90°,D是AC中点,∠ADF=∠CDB,连接CF交BD于E,求证:BD⊥CF.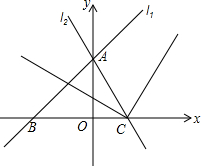 如图,平面直角坐标系中,直线l1:y=x+$\sqrt{3}$交x轴于B,交y轴于A,直线l2过点A交x轴正半轴于点C,并且OC:OB=1:$\sqrt{3}$,射线CE、CF分别为∠ACB及其外角的平分线.点M、N同时从A点出发,沿射线AB、AC方向运动.点M的运动速度为每秒$\sqrt{6}$个单位长度,点N的运动速度为每秒2个单位长度.直线MN与射线CE、CF交于点E、F,设运动时间为t秒.
如图,平面直角坐标系中,直线l1:y=x+$\sqrt{3}$交x轴于B,交y轴于A,直线l2过点A交x轴正半轴于点C,并且OC:OB=1:$\sqrt{3}$,射线CE、CF分别为∠ACB及其外角的平分线.点M、N同时从A点出发,沿射线AB、AC方向运动.点M的运动速度为每秒$\sqrt{6}$个单位长度,点N的运动速度为每秒2个单位长度.直线MN与射线CE、CF交于点E、F,设运动时间为t秒.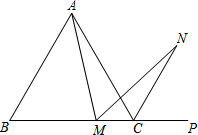 如图,在等边△ABC中,M为BC边上任意一点(不含B、C两点),P为BC延长线上一点,N是∠ACP的平分线上一点.已知∠AMN=60°,求证:AM=NM.
如图,在等边△ABC中,M为BC边上任意一点(不含B、C两点),P为BC延长线上一点,N是∠ACP的平分线上一点.已知∠AMN=60°,求证:AM=NM.