题目内容
2.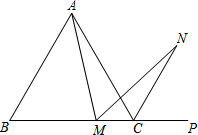 如图,在等边△ABC中,M为BC边上任意一点(不含B、C两点),P为BC延长线上一点,N是∠ACP的平分线上一点.已知∠AMN=60°,求证:AM=NM.
如图,在等边△ABC中,M为BC边上任意一点(不含B、C两点),P为BC延长线上一点,N是∠ACP的平分线上一点.已知∠AMN=60°,求证:AM=NM.
分析 在AB上截取EA=MC,连接EM,得△AEM,求出∠2=∠1,∠5=∠MCN,根据ASA推出△AEM≌△MCN即可.
解答 证明:在AB上截取EA=MC,连接EM,得△AEM,
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,
∴∠1=∠2.
又∵CN平分∠ACP,∠4=$\frac{1}{2}$∠ACP=60°,
∴∠MCN=∠3+∠4=120°…①
又∵BA=BC,EA=MC,
∴BA-EA=BC-MC,即BE=BM,
∴△BEM为等边三角形,
∴∠6=60°,
∴∠5=180°-∠6=120°,
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
$\left\{\begin{array}{l}{∠2=∠1}\\{AE=MC}\\{∠5=∠MCN}\end{array}\right.$,
∴△AEM≌△MCN (ASA),
∴AM=NM.
点评 本题考查了等边三角形的性质,正方形的性质和全等三角形的性质和判定的应用,解此题的关键是推出两三角形全等,题目比较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正方形ABCD的边长为4,正方形ECFG的边长为8,则阴影部分的周长为32.1,面积为24.(精确到0.1)
如图,正方形ABCD的边长为4,正方形ECFG的边长为8,则阴影部分的周长为32.1,面积为24.(精确到0.1)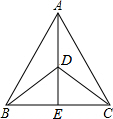 如图,在△ABC中,AB=AC,DB=DC,AD的延长线交BC于点E,求证:∠BAE=∠CAE.
如图,在△ABC中,AB=AC,DB=DC,AD的延长线交BC于点E,求证:∠BAE=∠CAE. 如图,在△ABC中,∠CAE=45°,F是高AD与CE的交点,BE=4,则线段EF=4.
如图,在△ABC中,∠CAE=45°,F是高AD与CE的交点,BE=4,则线段EF=4.
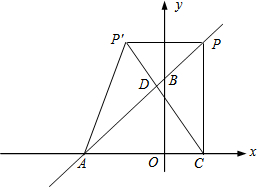 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-6,0),点B的坐标是(0,n)(n>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P′(点P′不在y轴上),连接PP′,P′A,P′C.设点P的横坐标为m.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-6,0),点B的坐标是(0,n)(n>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P′(点P′不在y轴上),连接PP′,P′A,P′C.设点P的横坐标为m.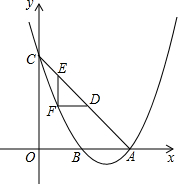 如图,当x=2时,抛物线y=ax2+bx+c取得最小值-1,并且抛物线与y轴交于点C(0,3),与x轴交于点A、B.
如图,当x=2时,抛物线y=ax2+bx+c取得最小值-1,并且抛物线与y轴交于点C(0,3),与x轴交于点A、B.