题目内容
1.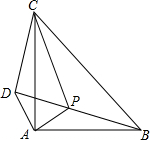 如图所示,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,将△PAB绕A逆时针旋转90°得△DAC.
如图所示,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,将△PAB绕A逆时针旋转90°得△DAC.(1)试判断△PAD的形状并说明理由;
(2)连接PC,若∠APB=135°,PA=1,PB=3,求PC的长.
分析 (1)结论:△PAD是等腰直角三角形.只要证明△BAP≌△CAD,即可解决问题.
(2))由△BAP≌△CAD,推出PB=CD=3,∠APB=∠ADC=135°,由△PAD是等腰直角三角形,推出∠ADP=45°,∠PDC=135°-∠ADP=90°,由AP=AD=1,推出PD2=AP2+AD2=2,在Rt△PDC中,根据PC=$\sqrt{C{D}^{2}+P{D}^{2}}$计算即可.
解答 解:(1)结论:△PAD是等腰直角三角形.
理由:∵∠CAB=∠PAD=90°,
∴∠BAP=∠CAD,
在△BAP和△CAD中,
$\left\{\begin{array}{l}{BA=CA}\\{∠BAP=∠CAD}\\{AP=AD}\end{array}\right.$,
∴△BAP≌△CAD,
∴PA=AD,
∵∠PAD=90°,
∴△PAD是等腰直角三角形.
(2)∵△BAP≌△CAD,
∴PB=CD=3,∠APB=∠ADC=135°,
∵△PAD是等腰直角三角形,
∴∠ADP=45°,∠PDC=135°-∠ADP=90°,
∵AP=AD=1,
∴PD2=AP2+AD2=2,
在Rt△PDC中,PC=$\sqrt{C{D}^{2}+P{D}^{2}}$=$\sqrt{9+2}$=$\sqrt{11}$
点评 本题考查旋转的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形,证明∠CDP=90°是本题的突破点,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.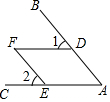 如图,点D、E分别在AB、AC上,若∠1=∠2=∠A=∠F,下列推理正确的是( )
如图,点D、E分别在AB、AC上,若∠1=∠2=∠A=∠F,下列推理正确的是( )
 如图,点D、E分别在AB、AC上,若∠1=∠2=∠A=∠F,下列推理正确的是( )
如图,点D、E分别在AB、AC上,若∠1=∠2=∠A=∠F,下列推理正确的是( )| A. | 由∠1=∠F得DF∥AE | B. | 由∠2=∠F得AD∥EF | C. | 由∠1=∠A得DF∥AE | D. | 由∠2=∠A得DF∥AE |
 如图,已知CD是⊙O的直径,AB是⊙O的弦且AB=16cm,AB⊥CD,垂足为M,OM:MC=3:2,则CD的长为20cm.
如图,已知CD是⊙O的直径,AB是⊙O的弦且AB=16cm,AB⊥CD,垂足为M,OM:MC=3:2,则CD的长为20cm.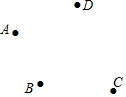 如图所示,平面上有四个点A、B、C、D,用直尺和圆规按要求作图:
如图所示,平面上有四个点A、B、C、D,用直尺和圆规按要求作图: