题目内容
18.如图,长方形ABCD中,E点在线段AD上,且BE=2AE,今分别以BE,CE为折线,将A、D向BC的方向折过去,若∠AED=15°,则∠BCE的度数为( )
| A. | 32.5° | B. | 45° | C. | 37.5° | D. | 30° |
分析 由题意得BE=2AE=2A′E,∠A=∠A′=90°,即可得△ABE、△A′BE皆为30°、60°、90° 的三角形,然后可求得∠AED′的度数,又由∠AED=15°,即可求得∠DED′的度数,继而求得∠BCE=∠2的度数.
解答 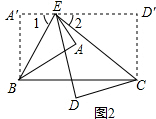 解:根据题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,
解:根据题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,
∴△ABE、△A′BE皆为30°、60°、90° 的三角形,
∴∠1=∠AEB=60°,
∴∠AED′=180°-∠1-∠AEB=180°-60°-60°=60°,
∴∠DED′=∠AED+∠AED′=15°+60°=75°,
∴∠2=$\frac{1}{2}$∠DED′=37.5°,
∵A′D′∥BC,
∴∠BCE=∠2=37.5°.
故选C.
点评 此题考查了翻折变换的性质、矩形的性质以及含30°角的直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意折叠中的对应关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 如图,已知正方形ABCD的边长为2,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°,得到点F,连接AF,则AF的最大值是( )
如图,已知正方形ABCD的边长为2,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°,得到点F,连接AF,则AF的最大值是( )
 如图,已知正方形ABCD的边长为2,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°,得到点F,连接AF,则AF的最大值是( )
如图,已知正方形ABCD的边长为2,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°,得到点F,连接AF,则AF的最大值是( )| A. | $\sqrt{13}$ | B. | $\sqrt{3}+2$ | C. | $\sqrt{5}+2$ | D. | $2\sqrt{2}+1$ |
6.下表是我国从1949年到1999年的人口统计数据(精确到0.01亿)
从表中获取的信息:
(1)人口随时间的变化而变化,时间是自变量,人口是因变量;
(2)1979-1989年10年间人口增长最慢;
(3)1949-1979这30年的增长逐渐加大,1979-1999这20年的增长先减小后增大;
(4)人口增长速度最大的十年达到约20%,
其中正确的有( )
| 时间(年) | 1949 | 1959 | 1969 | 1979 | 1989 | 1999 |
| 人口(亿) | 5.42 | 6.72 | 8.07 | 9.75 | 11.07 | 12.59 |
(1)人口随时间的变化而变化,时间是自变量,人口是因变量;
(2)1979-1989年10年间人口增长最慢;
(3)1949-1979这30年的增长逐渐加大,1979-1999这20年的增长先减小后增大;
(4)人口增长速度最大的十年达到约20%,
其中正确的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
 如图,两人从路段AB上一点C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地.且DA⊥AB,EB⊥AB.若线段DA=EB相等,则C是路段AB的中点吗?为什么?
如图,两人从路段AB上一点C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地.且DA⊥AB,EB⊥AB.若线段DA=EB相等,则C是路段AB的中点吗?为什么? 已知等边△ABC,点E是AB上一点,AE=3,点D在AC的延长线上,∠ABD+∠BCE=120°,tan∠D=$\frac{\sqrt{3}}{2}$,则CD=$\frac{9}{2}$.
已知等边△ABC,点E是AB上一点,AE=3,点D在AC的延长线上,∠ABD+∠BCE=120°,tan∠D=$\frac{\sqrt{3}}{2}$,则CD=$\frac{9}{2}$. 如图某玻璃碎片是梯形,已有上底的一部分,量得∠A=112°,∠D=98°,梯形另外两个角各是多少度?
如图某玻璃碎片是梯形,已有上底的一部分,量得∠A=112°,∠D=98°,梯形另外两个角各是多少度?