题目内容
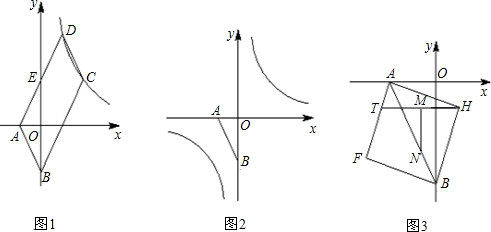
2.如图1,已知点A(b,0),B(0,a),且a、b满足$\sqrt{a+b+3}$+(b+1)2=0,?ABCD的边AD与y轴交于点E,且E为AD中点,双曲线$y=\frac{k}{x}$经过C、D两点.且D(m,4).(1)求m和k的值;
(2)点P在双曲线$y=\frac{k}{x}$上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,∠THN的度数是否会变化?若会的话,请给出你的证明过程.若不是的话,只要给出结论.
分析 (1)根据非负数的和等于0,可得这些非负数都等于0,从而可求出A、B的坐标,然后根据中点坐标公式就可求出m的值,再把点D的坐标代入反比例函数的解析式就可求出k;
(2)可分三种情况(AB、AP、AQ分别为对角线)讨论,然后只需运用中点坐标公式就可解决问题;
(3)过点N作NS⊥AH于S,作NR⊥AF于R,连接NH、NT,如图3.易证NR=NS,即可证到Rt△TRN≌Rt△HSN(HL),从而有∠RNT=∠SNH,由此可得∠TNH=∠RNS=90°,即可得到△TNH是等腰直角三角形,因而∠THN=45°(定值).
解答 解:(1)∵$\sqrt{a+b+3}$+(b+1)2=0,
∴$\left\{\begin{array}{l}{a+b+3=0}\\{b+1=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$,
∴A(-1,0),B(0,-2).
∵E为AD中点,D(m,4),
∴根据中点坐标公式可得xE=$\frac{{x}_{A}+{x}_{D}}{2}$=$\frac{-1+m}{2}$=0,
解得m=1,
∴D(1,4).
∵D(1,4)在双曲线$y=\frac{k}{x}$上,
∴k=1×4=4,y=$\frac{4}{x}$;
(2)若以点A、B、P、Q为顶点的四边形是平行四边形,
①当AB为对角线时,
根据中点坐标公式可得$\frac{{x}_{A}+{x}_{B}}{2}$=$\frac{{x}_{p}+{x}_{Q}}{2}$,$\frac{{y}_{A}+{y}_{B}}{2}$=$\frac{{y}_{P}+{y}_{Q}}{2}$,
则有$\frac{-1+0}{2}$=$\frac{{x}_{P}+0}{2}$,$\frac{0-2}{2}$=$\frac{{y}_{P}+{y}_{Q}}{2}$,
解得xP=-1,yP+yQ=-2.
∴yP=$\frac{4}{-1}$=-4,yQ=-2+4=2,
∴P(-1,-4),Q(0,2);
②当AP为对角线时,
同理可得P(1,4),Q(0,6);
③当AQ为对角线时,
同理可得P(-1,-4),Q(0,-6);
(3)当T在AF上运动时,∠THN的度数不会变化,等于45°.
提示:过点N作NS⊥AH于S,作NR⊥AF于R,连接NH、NT,如图3.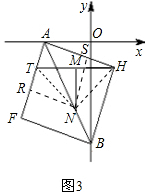
∵∠FAB=∠HAB=45°,
∴NR=NS.
∵M是HT的中点,MN⊥HT,
∴NT=NH,
∴Rt△TRN≌Rt△HSN(HL),
∴∠RNT=∠SNH,
∴∠TNH=∠RNS=90°,
∴△TNH是等腰直角三角形,
∴∠THN=45°.
点评 本题主要考查了二次根式的非负性、反比例函数图象上点的坐标特征、正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、中点坐标公式等知识,运用分类讨论是解决第(2)小题的关键,当然除用中点坐标公式外,也可通过构造全等三角形来解决第(1)题和第(2)题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2012 | B. | -2012 | C. | $\frac{1}{2012}$ | D. | $-\frac{1}{2012}$ |
| A. | 0.15×10-8 | B. | 0.15×10-9 | C. | 1.5×10-8 | D. | 1.5×10-9 |
 如图,AD∥BC,BD⊥BC,若∠ABD=25°,求∠A的度数.
如图,AD∥BC,BD⊥BC,若∠ABD=25°,求∠A的度数.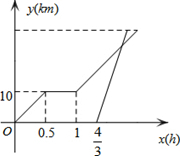 周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后,按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车速度是小明的3倍.
周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后,按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车速度是小明的3倍. 如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.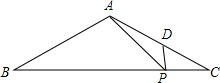 已知:如图,在△ABC中,AB=AC=13,BC=24,点P、D分别在边BC、AC上,AP2=AD•AB,求∠APD的正弦值.
已知:如图,在△ABC中,AB=AC=13,BC=24,点P、D分别在边BC、AC上,AP2=AD•AB,求∠APD的正弦值.